News

/img/uploads/2021/08/torusplane.webm

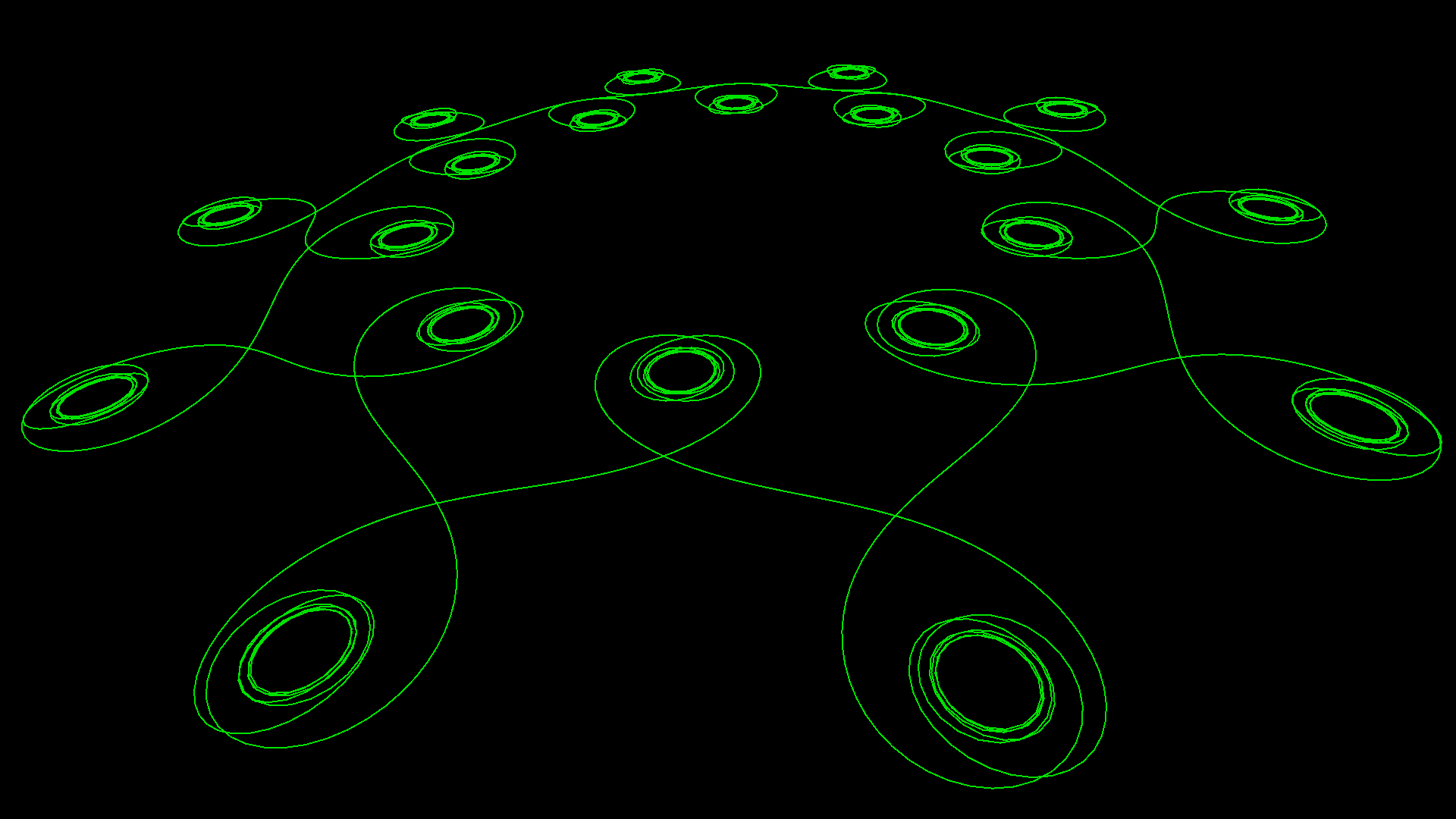
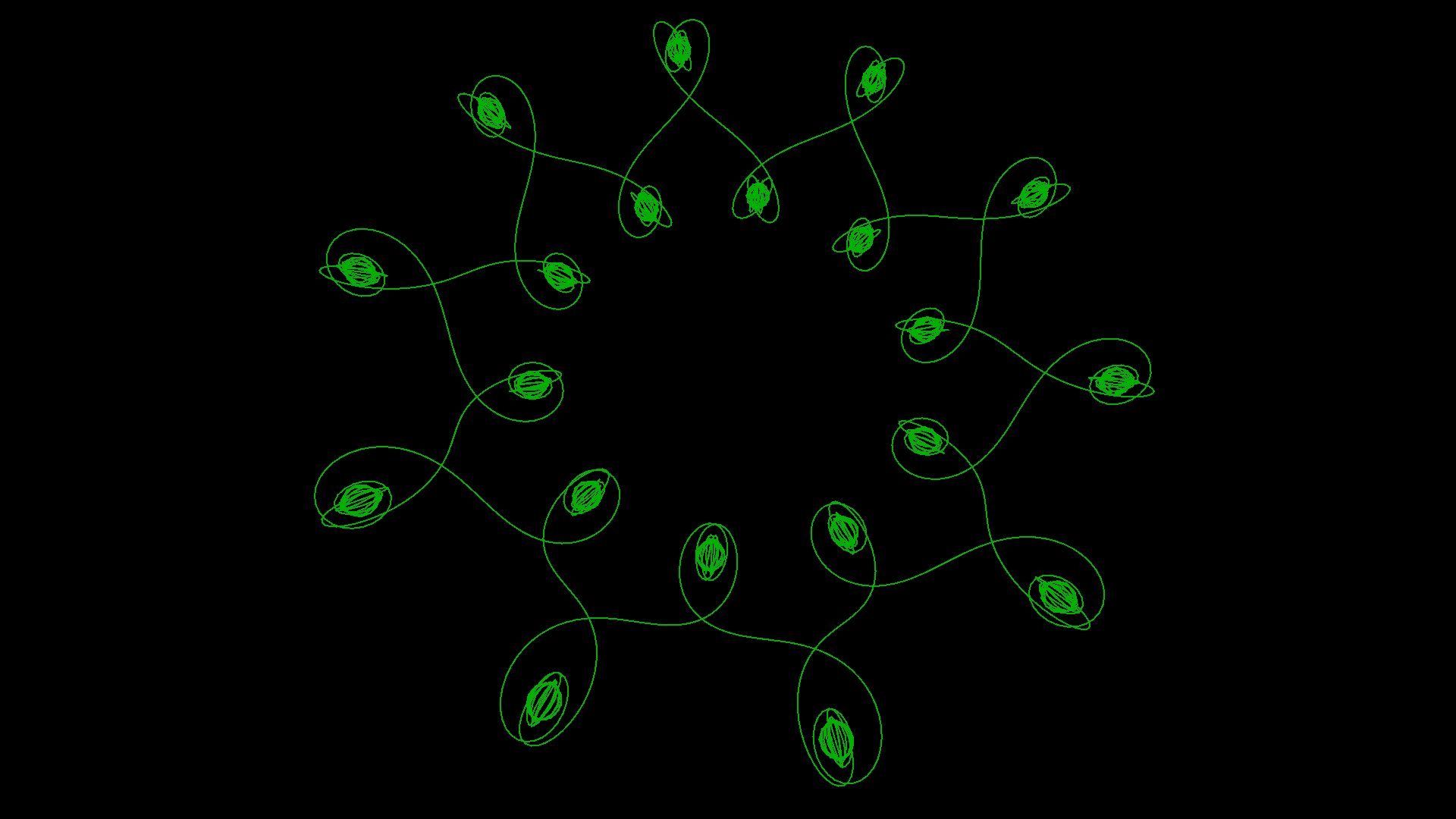
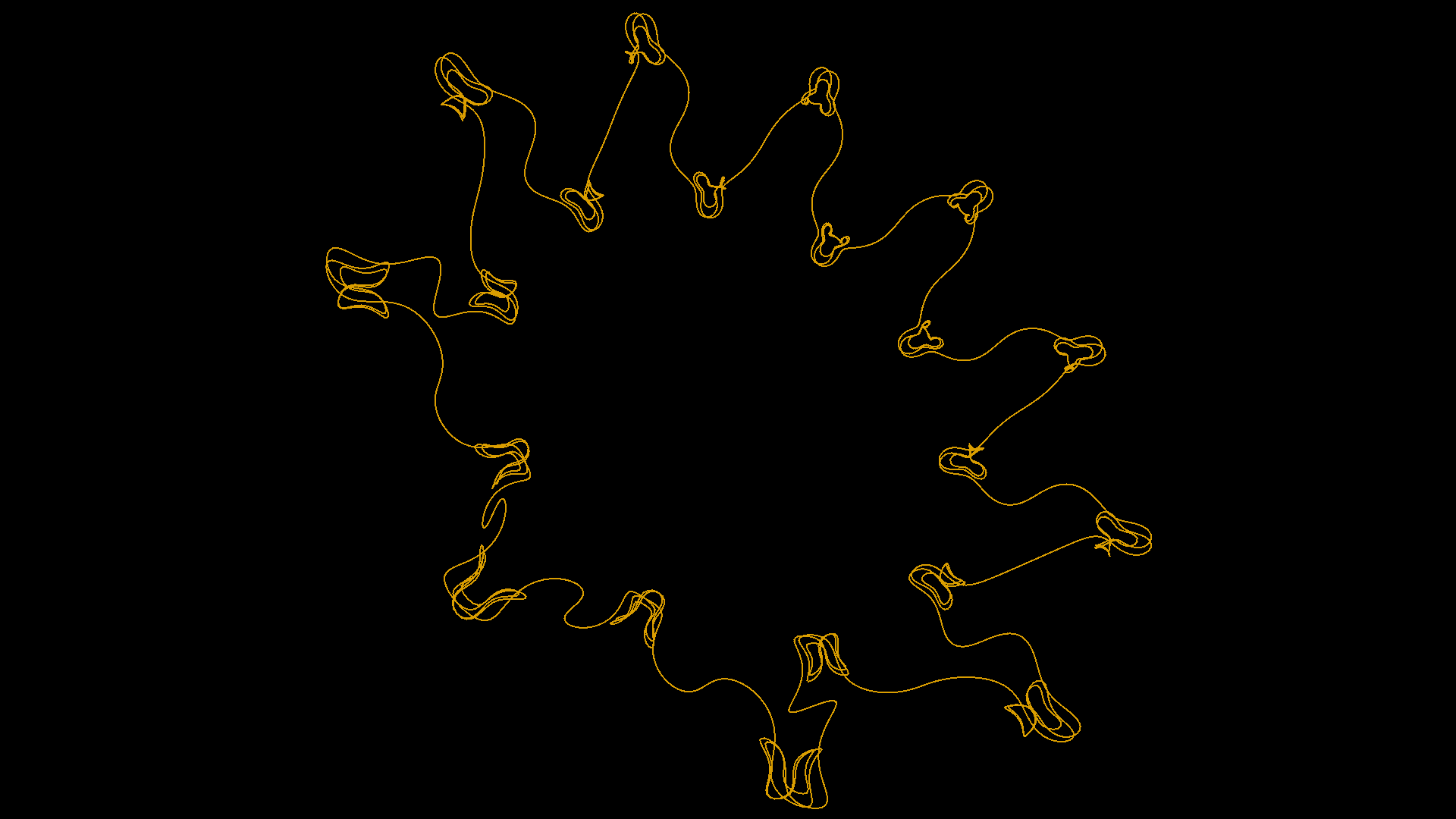
This example demonstrates the use of various camera-related functions, shape inversion, the premodel primitive and others to create this cool animation of a plane trapped in a torus!

The procedure first sets the turtle model to the built-in plane model, before creating a tag that sets the color of the torus. Then it creates an inverted torus (one whose inside is rendered instead of its outslde) because we’re going to fly inside it!

This guide is in development

Valid shapes:

Shapes must be closed, that is they must have no exposed ‘inside’ faces. Closed shapes include:

voxel, voxeloid, sphere, spheroid, icosphere, icospheroid, cappeddome, cappeddomoid, cylinder, torus, etc.

Note: the cylinders used for large pen sizes (rope) are valid shapes and appear to slice correctly.

Warning: open shapes will be rejected by your 3D printer’s ‘slicing’ software!

Making hollow forms:

To create a ‘hollow’ form, an inverted shape must be created within the outer shape. For example:

This simple commented project allows for the introduction of 3D movements and shapes (the rocket procedure) including a basic introduction to repeat, the creation of turtle models and the use of premodel, an introduction to the orbit primitives and the use of a new worker (thread) for orbiting the camera!

TO rocket
  forward 70
  down 90
  ;these two commands orient the rocket better for use as
  ;a turtle model
  
  setfillcolor yellow
  ;yellow is a function that returns the value 13
  ;it is a shortcut used for convenience in learning
  ;as is red, green, blue etc.
  
  cylinder 20 120 10
  ;cylinder takes   
  
  rollright 180
  ;flip the turtle over to create the nose cone
  
  cone 20 50 10
  
  lower 50
  ;lower the turtle to create the 'nose'
  
  setfillcolor red
  icosphere 3
  
  setfillcolor orange
  ra 50 + 120
  ;ra is short for raise
  
  rr 180
  ;rr is shorthand for rollright
  
  cutcone 20 30 30 10
  ;move the turtle to the bottom of the rocket and
  ;create the tail
  
  up 90 bk 30.1
  ;bk is short for back
  
  setfillcolor white
  repeat 2 [cylinderslice 40 5 20 10 rr 90]
  ;create the fins
  
  setfillcolor red
  dn 90 sl 10 bk 10 cylinder 10 10 10
  ;sl is short for slideleft
  
  fd 20 cylinder 10 10 10 sr 20
  ;fd is short for forward
  ;sr is short for slideright
  
  cylinder 10 10 10 bk 20 cylinder 10 10 10
  ;create the jets
  
END

TO createmodel
  clearscreen
  ;cs is short for clearscreen
  
  begintag "rocketmodel
  ;tags are used to create turtle models
  ;among other uses. You can also use them to
  ;show or hide parts of the 'turtle track'
  
  rocket
  ;run the rocket procedure
  
  endtag
  ;close the tag
  
  newmodel "rocket "rocketmodel
  ;create a new model called 'rocket' based on the
  ;rocketmodel tag
  
  setmodel "rocket
  ;set the turtle's model to the rocket model
  
  clearscreen
  ;clear away the tagged model, leaving only the
  ;turtle
END

TO starfield :number
  hideturtle
  norender
  ;suspend rendering of the scene until we're done drawing the stars
  penup
  repeat :number [
    home
    randomvectors randomfillcolor
    ;randomvectors orients the turtle randomly
    ;while randomfillcolor sets a random fill color
    
    forward 1000 + random 1000
    ;move forward a random distance
    
    up 90
    ;orient the turtle up in preparation of creating a spot
    ;because the spot is created around and below the turtle
    
    spot 10 + random 10
    ;create a randomly-sized spot
    
  ]
  
  home
  showturtle
  render
  ;resume rendering
  
END

TO main
  reset
  ;resets turtleSpaces to a default state
  
  createmodel
  ;execute the createmodel procedure
  
  starfield 200
  ;execute the starfield procedure, passing the parameter value 200
  
  setmodelscale 0.5
  ;decrease the size of the turtle model to half normal
  
  setpremodel [lt 90]
  ;inserts 'left 90' into the turtle track between the scene
  ;and the turtle model ('pre' the model)
  
  setfillcolor 14
  ;sets the fillcolor to 14. Type 'showcolors' or 'sc' in the console
  ;to see a list of default colors. You can also definecolor your own!
  
  ico 50
  ;create an icosphere (the planet)
  
  penup
  dropanchor
  ;set the 'anchor point', or the point the turtle 'orbits' around
  ;using the orbit commands, to the current turtle position
  
  pullout 80
  ;pull away 80 turtle units from the anchor point
  
  snappy:newworker [forever [orbitleft 0.1]]
  ;tell snappy the camera turtle to create a new routine or thread
  ;that forever orbits around the scene to its left one tenth of
  ;a degree at a time
  
  make "rotation 0
  ;define a container (variable) called 'rotation'
  ;and set it to 0. We're going to use it to keep track of the
  ;rotation of the rocket
  
  forever [
    inc "rotation
    ;same as make "rotation :rotation + 1
    ;there is also dec (decrement)
    
    setpremodel {"lt 90 "rollright :rotation % 360}
    ;curly braces indicate a 'softlist', a list that is evaluated
    ;at runtime. In this case, so that we can have a dynamic
    ;rotation value we pass to setpremodel
    
    ;% is shorthand for modulus
    
    orbitleft 1
    ;orbit the rocket one degree to the left
    
    wait 1
    ;wait one sixtieth of a second
    
  ]
END

What do Steve Wozniak and George H.W. Bush have in common? They’ve both been seriously into Tetris! But who can blame them? The object of the game (as if you didn’t know) is to complete horizontal lines using falling shapes of various configurations. When you finish a line, it disappears, causing the rest of the blocks to fall down a line. However, if you stack up shapes to the point they overflow the top of the playfield: Game Over. When you finish a certain number of lines, the level ends… and in the next, the shapes fall faster, and you need to complete more lines! The insanity never ends.

Check out this simple space invaders clone, featuring 3D UFO’s and UFO and player movement. This runs well on both the application and in the web version using modest hardware.

Rather than using hatchlings each with its own thread (worker), Invasion creates 15 static turtles representing each UFO, then iterates through moving them using the main (Myrtle) worker, more like a conventional single-threaded application would.

One procedure is used to generate randomly-colored UFO models, which are then assigned to each UFO turtle. The UFO turtles move in a 3D pattern created by ‘rolling’ them (rotating them on the Z axis), moving them left or right using slideleft and slideright, and raising and lowering them (using raise and lower) – a great exploration of 3D movement in turtleSpaces.

This simple yet attention-grabbing Logo procedure is a real visual treat, creating random three-dimensional ‘flowers’ based on the sine function. This could spice up a math class or just provide a brief introduction to sine waves in general.

Here is a simple Logo project to get started with. It creates a colorful filled hexagon pattern using the polyspot primitive.

The hexagon pattern zoomed out

TO hex
  
  clearscreen penup
  ;not drawing lines
  
  repeat 10 [
    ;do all of the following ten times
    
    setpos [-149 -270]
    ;sets the 2D turtle position (on the current Z plane)
    ;you can use setposition to set all three co-ordinates
    
    forward repcount * 34
    ;positions the turtle to start the line
    ;you could use some math with setpos to accomplish this
    
    randomfillcolor
    ;choose a random fill color
    
    polyspot 20 6
    ;make a filled polygon of size 20, with 6 sides
    
    repeat 10 [
      ;make ten more polygons
      
      slideright 30
      forward 17
      randfc
      ;randfc is the short form of randomfillcolor
      
      polyspot 20 6]
    ;return to the start of the loop
  ]
  ;finished
END

When I was a young child, one of my best friends was a turtle.

Not a real turtle, although that would have been fun, but a virtual one. My turtle lived inside of an Apple II, an early 8-bit computer, at my elementary school.

When I first met her, my turtle, she didn’t do much. She just sat there. It didn’t take long for me to realize that in order to get her to do something, I would need to prompt her. To do this, there was a literal prompt on the screen, beckoning me to type something.

▶ View interactive demo

Open in turtleSpaces IDERun starscape to create a galaxy of randomly-shaped and colored stars.

TO star :radius :points :size :filled
  ;takes number number number boolean (true or false)
  ;eg star 10 9 40 false
  ;or star 20 5 50 true
  
  pu dropanchor tether
  ;pull up the turtle pen, drop the 'anchor' to set the 'anchor point' to the current position, and do not change it if the turtle's rotation changes (tether)
  ;the anchor point is the point the orbit primitives orbit around
  
  if :filled [polyspot :radius :points * 2
    if oddp :points [rt 360 / :points / 4]]
  ;if creating a filled star, create a polygon to fill in the center
  ;if the star has an odd number of points, we need to turn a little
  
  pullout :radius
  ;pull out from the anchor point, which is currently the turtle's position
  
  repeat :points [
    ;repeat once for each point:
    
    pu make "position position
    ;set the :position container to the current turtle position
    
    orbitleft 360 / :points / 2
    ;orbit around the anchor point (in this case the center) to the left
    ;a fraction of 360 degrees divided by the number of points divided by 2
    
    pullout :size
    ;pull the turtle out from the center of the star (anchor point)
    
    setvectors direction :position
    ;point the turtle toward the previous position
    
    if not :filled [pd line distance position :position]
    ;if not making a filled star, create a line in front of the turtle of
    ;the length required for its end to be the previous turtle position.
    
    if :filled [frag]
    ;if creating a filled star, create a 'fragment' based on the last three
    ;turtle positions
    
    pu make "position position
    ;set the :position container to the current position
    
    pullin :size
    ;pull the turtle in toward the center of the star (anchor point)
    
    orbitleft 360 / :points / 2
    ;orbit to the left again a similar amound to the last orbitleft
    
    setvectors direction :position
    ;point toward the previous position
    
    if not :filled [pd line distance position :position]
    ;create a line if not a filled star similarly to the previous line
    
    if :filled [frag]
    ;create a fragment if a filled star similarly to the previous frag
    
  ]
END

TO starscape
  reset ht snappy:setposition [0 0 0] snappy:dropanchor repeat 200 [pu home randvec fd 1000 + random 1000 up 90 snappy:setvectors direction myrtle:position randfc randpc randps randfs star 10 + random 100 3 + random 20 10 + random 90 randbool]
END

In turtleSpaces, you can ‘stamp’ the current model, leaving a copy of it in the current position. This can be useful in some circumstances, to create artworks made out of more sophisticated models. In the case of this example, we’re going to use the default ‘myrtle’ turtle model to create a descending spiral of turtles.

If you change the colors in the default palette using the definecolor primitive, then those colors are also used to render the turtle model, and by extension the stamp. And so, if we ‘cycle’ the colors, shifting their RGB values from one palette slot to the next, we can create a rotating series of differently-colored turtles.