Logo isn’t just all about the turtles! When Logo was first being developed, there were no graphical displays — output was simple text on teletypes, which printed out interactions with the computer on paper. When the developers of Logo went into classrooms to test out their invention on students, all they had were teletypes.
As a result, the first Logo ‘microworld’ was the language microworld, not the geometry microworld which is more often associated with Logo. Logo was designed with many powerful commands used to manipulate strings and lists. Logo is based on Lisp, which stands for List Processing, a programming language in which data and code are the same, and are interchangeable and manipulatable by the running program. In Lisp, as in Logo, programs can modify, create and run themselves.
Some of these primitives (commands) include:
word – join two pieces of text together, eg word “dog “cat returns “dogcat
list – take two words and form a list, eg list “dog “cat returns [dog cat]
first, second, third, last – returns the appropriate character (word0 or item (list)
item, setitem – retrieve or change an item in a list or word based on its numerical index
fput, lput – returns a copy of a list with an additional item inserted in the front or back
butfirst, butlast – returns a list without the first or last item
leading, trailing – returns the front and back of words, respectively
push, pop, queue, dequeue – add or remove items on to the front or back of lists
There are also primitives that sort and search, retrieve words from a built-in English dictionary, convert characters to ASCII and back, and much more. You can browse them all in the Words and Lists reference.
So what can we do with all of these wonderful, powerful tools? Here’s a few examples:
Output
While we can manipulate strings and lists internally we still need to output the result to the user. In Logo, this can be done using the show, print and type primitives, and in turtleSpaces you can additionally typeset (create graphical text) or say (text-to-speech) them.
This example uses the print and the pick commands, the former types text into the console (text) area, following it with a line feed (carriage return) while the latter chooses (picks) a random item from a supplied list. In the example, this is used to generate a randomized simple story:
TO simplestory
;this language module contains a number of
;different procedures that manipulate language
;in fun ways!
;For example, this procedure uses the print
;and pick primitives to choose randomly from
;a series of lists, creating a simple one-line
;story:
(
;encompassing the print command
;in round brackets allows us to supply it
;more parameters than normal. This also
;works with commands like say and functions
;like word and sentence
print "The
pick [
red green blue
]
pick [
frog cow cat
]
pick [
jumped ran walked
]
pick [
|over to| over underneath
]
;to create a "word with spaces" (a phrase) in a list,
;a single list item containing spaces,
;enclose it with pipe symbols.
"the
word pick [
overpass mountain |shopping mall|
] ".
;word is used here to create a single word
;made up of the final 'pick' and a period.
)
END
Note that a ‘word’ in Logo is a single word, usually represented with a single double quote, eg “frog
Multiple words can either be represented in a list, eg [dog cat pig], or as a phrase |fat dog|, or both [|fat dog| |lazy cat| |pink pig|]
In the case of the last example, the second item in that list is |lazy cat|. You can turn |lazy cat| into a list of two items using the parse primitive.
A one-line version:
TO oneline
; a simple single line 'story':
print (sentence pick [|The duck| |Old John| |A tabby cat| |Little Susie|] pick [ran walked surfed jumped danced] pick [|away from| towards] pick [|the city| |the mall| |their house|])
END
Questions and Answers, Repeats and Repcounts
The next example takes a user-supplied string and turns it into a word pyramid, by repeatedly displaying more and more of the word on successive lines.
It does this first by retrieving the desired word from the user using the question primitive, which prompts the user for input and then ‘stores’ the result in the ‘answer’ primitive, a function that returns the user’s input.
Then, it determines the length of the word using the count primitive, and employs repeat and repcount to generate the pyramid. repcount returns the current iteration of a repeat loop and is a very useful primitive.
reverse is also used in this example, which reverses a word or list.
TO wordpyramid
;this procedure creates a text 'pyramid'
;out of a string provided by the user:
question |word| make "word answer
;the question primitive prompts the user
;for input, which is retrieved using the
;answer function
;the make primitive places the output from
;answer (the input to question) in a container
;called "word, which is read using :word
repeat count :word [
;count is a function that returns the number
;of characters in the provided word, which is
;in this case the contents of the "word container
;symbolized using :word (which is the equivalent
;of 'thing "word', the primitive 'thing' able
;to retrieve and return the contents of containers.)
repeat (count :word) - repcount [
;expressions are resolved right to left. What
;this means is that without the round brackets,
;Logo would try to subtract repcount (which returns
;the current number of repeat loop iterations)
;from the contents of the :word container, a string,
;which would result in an error. We solve this by
;placing round brackets around (count :word) to
;ensure that repcount is subtracted from the
;result of count :word instead
type spacebar
;'type' prints a character(s) without adding a
;carriage return at the end, allowing one to type
;more on the same line. spacebar is a function that
;returns the space character
]
if repcount = 1 [
;if the current repeat iteration is 1 (the first):
print first :word
;print the first character of the contents of the :word container
] [
;otherwise:
print (word
;print a word made up of:
reverse leading repcount :word
;the leading (first) repeat loop iterations characters
;in the :word container, but in reverse.
;Remember, Logo evaluates expressions from right to left,
;so it first slices off the first however many 'leading'
;characters from the front of :word and then reverses it.
butfirst leading repcount :word
;the second part of our combined word is the leading
;repcount number of characters, excluding (butfirst)
;the first character.
)
]
]
;don't forget you can hover the mouse over keywords to
;get a popup that explains what they do!
END
Word(s) around the world!
The turtle is starting to get a bit bored, so let’s give her a bit of a workout! The next example uses the typeset and orbit primitives to create a ‘word circle’ out of user-provided input.
The orbit commands in turtleSpaces allow the turtle to orbit around a specific point in turtleSpace. We’re going to use the item primitive and a bit of math to distribute the input into a ring around the home [0 0 0] point:
TO wordcircle
;this procedure create a graphical 'word circle'
;out of the supplied word:
clearscreen hideturtle
dropanchor penup question |word|
;dropanchor moves the 'anchor point'
;used by orbit primitives to the turtle's
;current location
pullout 8 * count answer
;pullout backs the turtle away from the
;anchor point without moving it with
;the turtle
;in this case, we're 'pullling out'
;8 turtle-units * the number of characters
;in the 'answer' provided to the question
;by the user
repeat count answer [
;loop for however many characters are in the answer:
randomfillcolor
typeset item repcount answer
;typeset (create a graphical character) for the
;character 'item' in the place of the current repeat iteration
;eg if the word was 'frog', item 1 is 'f', item 4 is 'g'
;and on the third loop iteration it would be 'o'.
slideleft 10
;the turtle moves when it typesets the character, but
;we're going to 'orbit' to make a circle, so we need to
;move the turtle back to where it started
orbitright 360 / count answer
;'orbit' the turtle 360 degrees divided by the number of
;letters in the answer
]
;all done creating the circle
forever [
cam:rollright 1 wait 1
]
;rotate the camera forever
END
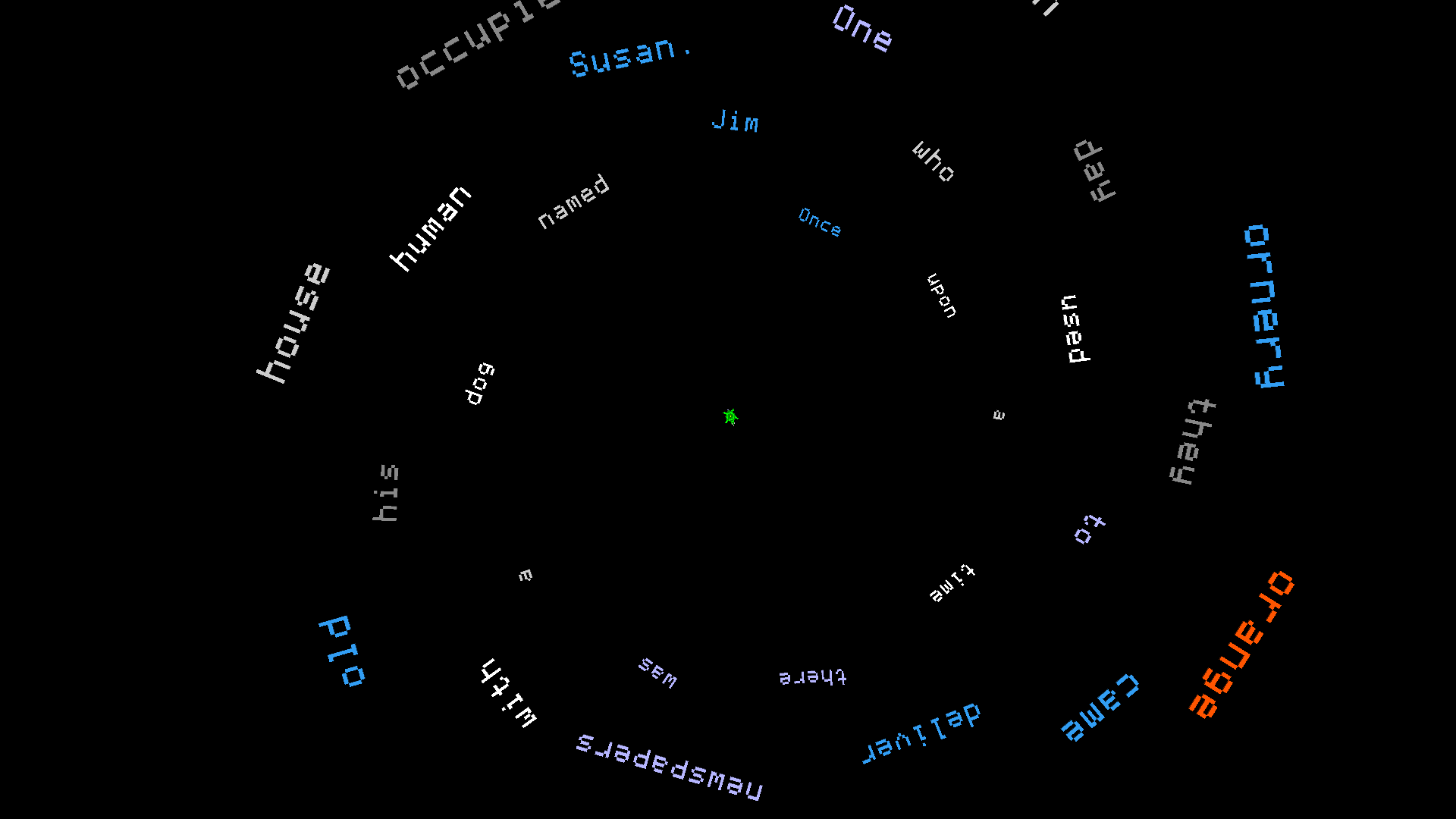
Spiral Stories
Similarly, this next example creates a spiral of words, which grow larger over time as the spiral is built. Each word is spoken by the computer’s text-to-speech facility. Rather than prompting for input, the ‘story’ is defined in a container (variable) using the make primitive.
While in the previous example, item was used to pick out each letter in the user’s input, here it is used to pick out each list item (word) in the “message (story) container.
The foreach primitive is used to typeset each letter in each word independently, to create a more flowing effect. This example demonstrates opportunities for creating text-based animations and artworks:
TO wordspiral
;creates a spiral made out of words from a given message:
reset
cam:pullin 100
;pulls the camera closer to the turtle
cam:tandem myrtle
;causes the camera to match the turtle's movements
penup
;don't draw lines
make "message [Once upon a time there was a dog named Jim who used to deliver newspapers with his human Susan. One day they came upon an old house occupied by an ornery orange cat.]
;sets the message into the :message container.
;The message is a list of words,
;as opposed to a single word
repeat count :message [
;repeat the following the same number of times
;as there are words in the message:
cam:pullout 10
repeat 19 [
right 2 cam:rollright 2 wait 1
]
;turn in an animated way
settypesize 10 + (repcount / 2)
;make the words larger as we progress
if repcount = 32 [
setfillcolor orange
;if this is the 32nd word, make the
;'fillcolor' orange
] [
;otherwise pick one from the given list:
setfc pick [6 7 5 10 15]
;many primitives have shorter 'shortcuts'
]
;the fillcolor is the color used to create
;shapes such as typeset characters
say item repcount :message
;speak the current word
foreach "i item repcount :message [
;for each letter in the current word:
typeset :i wait 1
;typeset the letter and wait 1/60th of a second
]
if repcount != count :message [
;if this isn't the last word:
repeat 12 - count item repcount :message [
;repeat 12 subtracted by the number of letters in the word:
typeset spacebar wait 1
;type a 'space' and wait 1/60th of a second
]
]
]
;if we're here, we're finished the spiral!
wait 120
setxy -100 -150
;move the turtle to the center
cam:notandem
repeat 480 [
cam:pullout 1 cam:rollright 1 wait 1
]
;spin the camera and pull it back
END
Codes and Cyphers
Whew! Myrtle’s had her workout, so she can take a well-deserved rest now. Let’s look at some fancier text manipulation, starting with a simple cypher.
Cyphers traditionally manipulate each letter in words in a specific, usually secret way, so that one can pass messages without those who intercept them having the ability to read them.
In the case of our simple example, we’re going to advance the ASCII value of each character by one, changing A into B and so-on.
This procedure is also our first encounter (in this article anyhow) with the “functionalisation” of a procedure in Logo.
In Logo, a procedure can either be just a procedure, in the sense that it is executed simply by declaring its name, and nothing more, or it can be a function, which requires input values be provided when it is declared, such as forward 20. It can also be a returner, which returns a result but requires no input, or a functional returner, which takes input and returns a result.
clearscreen – procedure
forward 20 – function
pencolor – returner
sin 20 – functional returner
Our cypher is a functional returner: it requires an input while returning an output. As a result, it needs to be executed by feeding it back into something else, such as print:
print cypher “albatross
This cypher example only encrypts a single word, or phrase if input is provided using the pipe symbols:
print cypher |I wish I was a secret agent!|
Now, as to the code itself, it first uses a boolean (listp) to check if the input is in fact a word / phrase and not a list, and complains if it is not. Booleans (predicates, which is why they typically end with p) return true or false, based on the input they are provided or the state of the turtleSpaces environment. The ‘if’ primitive takes a boolean result and if it is true then executes the supplied list.
See what I mean when I say lists of data and code are the same in Logo? You can manipulate lists of code just like any other list, and attempt to execute any list (although the results may not be that useful!)
Next we create an empty output container, and then foreach character in the input, we convert it to its ASCII value, add one, and then convert it back into a character, inserting it into the output container. Finally, we use the output primitive to return the result back to the calling primitive, for example print.
TO cypher :input
;A simple cypher:
;adding a :parameter to the end of a TO declaration
;causes the procedure to require the parameter when it
;is called.
;in this case, we're requiring a parameter called :input
;which when provided will place that given value into
;a container called :input _that only exists for the
;time this procedure is executed_ then vanishes!
if listp :input [print |You can only provide a word to this procedure!| stop]
;check to see if the input is a list. If it is, reject it
;and stop processing this procedure
make "output "
;initialize an empty container called :output
foreach "letter :input [
;for each character in the :input container
;(represented by :letter) :
make "output word :output char (ascii :letter) + 1
;update the :output container to contain the current contents
;of that container plus:
;the character representation of
;the ASCII value of
;the current :letter
;plus one.
;So, for example, the ASCII value of A is 65. We're
;going to add one to that (66) and then add the char(acter)
;representation (B) of that ASCII value to the existing :output
;container
]
;We do this for all the letters in the supplied word.
output :output
;we 'return' our finished :output via the output command.
;This means that the output is passed on to the next command
;rather than just being printed out. It makes this procedure
;a _function_. Functions take input and return output.
;So, to show our cypher, we must enter a command such as:
;print cypher "elephant
;because if we just type: cypher "elephant
;Logo will not know what to do with the output
END
Deciphering the Gibberish
Of course we need to decipher our encrypted messages too:
TO cypherlist :input
;this function takes a list rather than a word,
;and uses cypher to encrypt each word separately:
local "output
;we use :output in 'cypher', so we need our own
;'local' copy that is exclusive to this procedure
;and will not be modified by 'cypher'
make "output []
foreach "i :input [
queue cypher :i "output
]
output :output
;can you write a 'decypherlist'?
END
The Language of Music
Of course, English isn’t the only language Logo can speak — it can speak all sorts of languages! But especially, it can speak the language of music, using the playnotes primitive.
playnotes takes a list of music ‘commands’ and then plays them. These include:
L# – play the next provided note at the given length. L0 = 16th note … L9 = double whole note!
R# – plays a ‘rest’ (no tone) of the given length (similar to L)
C5 – plays a note of the given tone (C) and length (5)
Can we use list primitives to create random music? You bet we can!
This example uses the forever loop to play randomly generated music… forever! Inside the forever loop the code employs the list, word, pick and random primitives to piece together our computer-created composition:
TO randommusic
;but hey, all word and list handling isn't necessariy
;about text. Check out this random music generator:
forever [
(
playnotes (pick
;pass to the playnotes primitive (which plays
;musical notes) one of the following two things:
;either:
list (list word "R random 6)
;a list (which is the type of data playnotes
;requires) made up of a single word containing the
;letter R and a random number between 0 and 5,
;the combined word (eg R4) signifying a rest, or:
(list
word "L random 6
word pick [C# D# F# G# A#] pick [3 4 5 6]
)
;a list made up of two words, the first containing
;the letter L and a number between 0 and 5,
;and the second containing a note (eg C#) and
;an octave (eg 4)
)
;use round brackets to space out your command statements
;across multiple lines, to make them easier to read
;and explain!
)
]
END
Note how we can use the () round brackets to spread out a single complete instruction across multiple lines to make it easier to comment and read.
Doyay owknay igpay atinlay?
Pig Latin is a perennial favourite of children across the ages. A series of simple rules are used to create a ‘secret language’ that can only be understood by those who know them.
The rules are:
- If the word only has one letter (a) leave it as-is
- If the word only has two letters, add ‘yay’ to it
- If the world starts with ‘th’, move it to the end and add ‘ay’ to it
- If the word starts with a vowel, add ‘nay’ to it
- Otherwise, move the first letter to the end and add ‘ay’ to it.
The following example uses if, elsif and else to sort the input words through all of these rules, stitching together a result:
TO piglatin :input
;doyay owknay igpay atinlay?
;this procedure takes a list as an input
make "output []
;initialize the output container as an empty list
foreach "word :input [
;for each word in the input string:
if 1 = count :word [
;if the word only has one letter (a):
queue :word "output
;put it in the output untouched
]
elsif 2 = count :word [
queue word :word "yay "output
]
;if the word is two letters, add it to the output
;+ 'yay'
elsif "th = leading 2 :word [
;otherwise, if the word starts with 'th':
queue (word trailing (count :word) - 2 :word "thay) "output
;take the remaining part of the word minus the 'th' and add 'thay' to it
;then 'queue' it (add it to the end of) into the :output list
]
elsif not memberp first :word [a e i o u y] [
;- 'not' reverses the boolean, making a true false
;- 'memberp' returns true if the first value provided to it
;is present in the list supplied as the second value
;and so, if the first letter in the word is NOT
;a vowel:
queue (word butfirst :word first :word "ay) "output
;take everything except the first letter (butfirst)
;and then add the first letter to the end, followed
;by "ay, Note the brackets around the word function,
;they are needed because we are supplying three
;inputs: the end of the word, the first letter and "ay.
;finally we queue the result into :output
]
else [
;FINALLY, if all else fails (the word starts with a vowel):
queue (word :word "nay) "output
;we think you can figure this one out for yourself! :)
]
]
show :output
;we're going to show the output rather than outputting it,
;but you could change this to output :output if you wanted
;to use this as a function.
END
Note the use of the leading and trailing primitives, which return the front and back of input words, respectively.
And now for something (somewhat) completely different…
You know that you can make containers containing values, and that you can use expressions to create those values. Typically these expressions are evaluated before they are put into the container, and so they are fixed at the point in time the make is executed. But what if you could put the expression into the container instead? This is where make! comes in handy:
TO nameexample
;this is a brief example of make!
;which creates a container whose value can be different
;every time you 'look' in it! (hence make!)
;in this case, when we define our container using
;make!, the expression goes into the container, not the result.
;This means that every time we show the container's 'contents'
;what we get back is an evaluation of the expression. So if
;we provide a dynamic expression, then the result will be
;varied.
make! "name sentence pick [Big Little Stout Thin Tall Short] pick [Jim Fred Mark Paul Mike]
show :name
show :name
show :name
make! "time (se hours minutes seconds)
show :time
END
As you can see from the example, containers created with ‘make!’ are more like magic boxes, whose contents change based on when you look inside them. Logo is magical, indeed!
A Sophisticated Story
Earlier, we told a simple story, now let’s tell a more sophisticated one.
In the following example, a series of list containers are created containing various story elements. These elements are then laid out on the graphical display using the typeset primitive. Note the absolute positioning set using the setxy primitive.
This is actually a fairly simple example, with the opportunity for participation from the entire classroom, in choosing the various words and phrases that make up the story:
TO story
;Let's tell a random story. This can be a fun yet simple project for students
;since they can pick the various items that go into each list of story elements:
make "protagonist [|an old man| |a young lady| |a small dog| |a white cat| |a red walrus|]
make "city [Vancouver Seattle |Los Angeles| |New York| Paris Rome]
make "vehicle [|their car| |their bike| |the bus| |a taxi| |an Uber|]
make "destination [supermarket mall dentist |computer store| |art gallery|]
make "badevent [|slipped and fell| |got mugged| |lost their wallet| |got sick|]
make "goodevent [|found $100| |won the lottery| |met Ryan Reynolds| |ate a burger|]
;first we 'make' lists for each element in the story
;note that phrases (also called 'long words') have to be surrounded with pipes ||
clearscreen penup setxy -200 100
;setxy positions the turtle at the given x and y co-ordinates
settypesize 9
typeset (sentence |There was once| pick :protagonist "from word pick :city ",)
;sentence assembles multiple words into a list (including 'long words' or phrases)
;we're using word here to add punctuation to a word (or phrase) taken from the :city list.
setxy -200 80
typeset (sentence |who took| pick :vehicle |to the| word pick :destination ".)
setxy -200 60
typeset (sentence |Sadly, they| word pick :badevent "!)
setxy -200 40
typeset (sentence |But luckily, then they| word pick :goodevent "!)
setxy -200 -50
typeset |And they lived happily ever after.|
home
END
And they lived happily ever after.
The next word, and the next word…
This next example is a simple little cracker, which uses the english primitive to retrieve random words from turtleSpaces built-in English dictionary, and then typesets them into the graphical display, rolling and turning the turtle to create a 3D ‘word cloud’.
If you click and drag on the graphical display area you can rotate around the output.
TO wordcloud
;creates a 3D word cloud out of random words:
clearscreen penup
repeat 100 [
right pick [-90 90]
typeset pick english 6
;'english' returns a list of english words of the given length
slideright 10 rollright 90
]
END
If you are unable…
The next example tries to pick a random word out of the dictionary and turn it into an un-able variation, eg unfixable.
A naive version would look something like:
print (word “un pick english 5 “able)
which while straightforward is going to output a lot of rubbish.
Like piglatin, we’re going to define some rules that we’ll use to process the word and see if we can create something that makes sense. But this time we’re going to do this through exclusion — if the random word doesn’t conform to our rules, we will simply pick another one.
We’ll do this using the dountil primitive, which does something until specific conditions are met:
TO unable
;tries to create the 'un-able' version of a random word, eg unstoppable
;A simple version:
;print (word "un pick english 5 "able)
;stop
;A better version:
dountil (
;we're going to cheat and find a good un-able word:
;'dountil' means perform the provided list, THEN
;check the conditions, and if they are false, perform
;the provided list of instructions AGAIN until the
;conditions are all true.
and
;do this until all of the following are true:
"un != leading 2
;the first two letters aren't 'un' -- we don't want 'ununable'
:pick "er != trailing 2
;the last two letters aren't 'er' -- that would just be weird
:pick not memberp last :pick [a e i o u y s d g]
;the last letter isn't a vowel or s, d or g
;note that the opening round bracket beside 'dountil'
;has allowed us to spread the above out across multiple lines.
;Without the brackets, all of that would have needed to be
;on the same line, or Logo would have become confused.
) [
make "pick pick english 6
;pick an english word with 6 letters and place it into
;the :pick container
]
print (word "un :pick "able)
;print the un-able word
END
Is this cheating? We’ll leave that for you to decide.
Check out these and other examples in the following turtleSpaces project:
turtlespaces.org/weblogo/?pub=193