Tag logo programming

Spaces contain subsets of the broader turtleSpaces primitive (keyword) set dedicated to various types of creation. They also have restricted feature sets, to enable gradual exposure to everything turtleSpaces has to offer.

You can select a Space from the menu provided by clicking on the name of the current Space (eg omniSpace) in the top-left corner of the web IDE, or by clicking on the link in the following list:

welcomeSpace (2D) – a very simple Space with only basic turtle commands and no editor

penSpace (2D) – has a simple editor and the subset of turtle pen commands

wireSpace (2D) – like penSpace but in three dimensions

artSpace (2D) – adds the ability to create fills (arbitrary 2D shapes) and other goodies

designSpace (2D) – adds shapes and text fonts

animationSpace (2D) – adds movement capabilities

physiSpace (2D) – adds 2D physics functionality

actionSpace (2D) – adds missiles, objects and other game-related functionality

textSpace – dedicated to text / list manipulation

musicSpace – dedicated to MIDI music creation

omniSpace – everything!

To come:

modelSpace (3D) – assisted 3D model creation

motionSpace (3D) – 3D animation

(simulationSpace, virtualSpace…?)

Each Space also has its own published / example database containing projects that use the keywords available in the Space.

In turtleSpaces, you can ‘stamp’ the current model, leaving a copy of it in the current position. This can be useful in some circumstances, to create artworks made out of more sophisticated models. In the case of this example, we’re going to use the default ‘myrtle’ turtle model to create a descending spiral of turtles.

If you change the colors in the default palette using the definecolor primitive, then those colors are also used to render the turtle model, and by extension the stamp. And so, if we ‘cycle’ the colors, shifting their RGB values from one palette slot to the next, we can create a rotating series of differently-colored turtles.

Note: For reasons, colors 0 (black) and 15 (white) cannot be redefined. But there are 1-14 and 16-63 to play with, which is plenty!

For aesthetic reasons, we want a certain turtle to have the default colors, so we need to add an offset to some of the calculations to make that happen. Finally, we need to position Snappy (the camera or view turtle) in a certain position to get the view we want. Because this involved a fair amount of manual fiddling, I’ve just inserted the position and vectors into the listing to reproduce Snappy’s position and orientation.

Finally, to make the spiral we’re going to use the orbit commands, which rotate the turtle around an ‘anchor point’. The tether primitive allows us to turn the turtle away from the anchor point, which would normally move the anchor point but does not if tether is called. We descend a little each time we move, creating a downward spiral.

TO turtlesallthewaydown

  reset
  
  snappy:setposition [-0.0567188571145 -41.2097873969 -9.14256453631]
  snappy:setvectors [
    [0.0177688320245 0.192937058466 -0.981050233209]
    [-0.00350577343795 0.981211134942 0.192905205264]
    [0.999835975629 1.16396598173E-05 0.0181113694522]
  ]
  ;position Snappy where we want him to reproduce the image
  
  make "defaultcols colors
  ;make a copy of the default color palette
  
  penup dropanchor
  pullout 50 tether
  ;we want 'orbit' in a circle
  
  left 90 orbitright 39
  ;because we tethered, we can point away
  ;then orbit around the anchor point
  
  repeat 800 [
    setfillshade -5 + repcount / 20
    ;set the shade of the fill color, the color used
    ;to create the voxels that make up the turtle, amongst others
    
    make "offset remainder repcount + 11 14
    ;why +11? So we get the default turtle colors in the right place!
    
    repeat 14 [
      definecolor repcount item 2 + remainder (:offset + repcount) 14 :defaultcols
      ;shuffle the color palette. We need to start at item 2 because 1 is black
      ;(item is 1-based, whereas definecolor is 0-based -- 0 being black)
      
    ]
    
    stamp "myrtle
    ;make a copy of myrtle in the current position
    
    orbitleft 22.95 lower 1
  ]

END

If you replace stamp “myrtle with stamp “astronaut, and before it add a setmodelscale 0.5, like this:

setmodelscale 0.5 stamp "astronaut

you get:

If you change the “astronaut in stamp “astronaut to stamp pick [astronaut spaceship plane] like so:

setmodelscale 0.5 stamp pick [astronaut spaceship plane]

you’ll get:

Today’s example is short but sweet. It creates a design made out of a bunch of qtip-like ‘sticks’ with balls on the ends.

It is a design made out of ‘almost squares’ (four sides each at an 85 degree angle to each other). The turtle then turns right 5 degrees, and slides left 20 before continuing to the next almost-square.

Each side of the almost-square is coloured based on its iteration in the almost-square loop, and the fill colour of the balls is set to match. Also, each iteration is raised an amount relative to its iteration, creating a pleasing 3D effect.

Click here to open the project in the viewer or open it in the webLogo IDE

TO qtips
  hideturtle
  clearscreen
  repeat 24 [
    repeat 4 [
      penup 
      setz repcount * 3 
      ;raise up the turtle based on the loop count
      pendown 
      setpencolor 10 + repcount
      ;set the pen color based on the loop count
      setfillcolor pencolor 
      ;for the spheres
      icosphere 2 
      rope 100 
      ;a rope is a cylinder-based line
      icosphere 2 
      right 85
    ] 
    right 5 
    penup
    slideleft 20 
    pendown
  ]
END

Sierpinski’s Gasket

These routines use recursion (they repeatedly call themselves) to realise different Sierpinski algorithms. Logo’s recursion capabilities and relational turtle make it excellent for the task of rendering these algorithms! They’re also very pretty.

TO half_s :size :level
  if :level = 0 [fd :size stop]
  half_s :size :level - 1
  lt 45 fd :size * sqrt 2 lt 45
  half_s :size :level - 1
  rt 90 fd :size rt 90
  half_s :size :level - 1
  lt 45 fd :size * sqrt 2 lt 45
  half_s :size :level - 1
END

TO sierpinski :size :level
  repeat 2 [
    half_s :size :level
    rt 90 fd :size rt 90
  ]
END

TO sierp
  cs pu back 180 pd sierpinski 3 5
END

sierp

Instead of drawing lines, we can construct triangles out of ‘pins’ dropped at appropriate points:

TO half_s :size :level
  penup
  if :level = 0 [fd :size stop]

  pin
  ;pin marks a point for use with pinfrag

  half_s :size :level - 1
  lt 45 fd :size * sqrt 2 lt 45
  half_s :size :level - 1
  rt 90 fd :size rt 90
  half_s :size :level - 1
  lt 45 fd :size * sqrt 2 lt 45
  half_s :size :level - 1

  pinfrag
  ;creates a triangle out of the last three 'pins'

END

sierp

We could drop twice as many pins and then select a color for each ‘frag’ (fragment) triangle from a list:

TO half_s :size :level
pu
if :level = 0 [fd :size stop]

pin
;drop pin

half_s :size :level - 1
lt 45 fd :size * sqrt 2 lt 45
half_s :size :level - 1

pin 
;drop another pin

rt 90 fd :size rt 90
half_s :size :level - 1
lt 45 fd :size * sqrt 2 lt 45
half_s :size :level - 1

setfc item :level [9 8 1 13] pinfrag
;pick a color from a list based on the current level and create the fragment

END

sierp

Sierpinski’s Triangle

It’s triangles all the way down!

TO sierpinski :size :level
  if :level > 0 [
    rt 30
    repeat 3 [
      fd :size
      rt 120
    ]
    left 30
    sierpinski :size / 2 :level - 1
    rt 30
    fd :size / 2
    left 30
    sierpinski :size / 2 :level - 1
    rt 30
    back :size / 2
    left 30
    rt 90
    fd :size / 2
    left 90
    sierpinski :size / 2 :level - 1
    left 90
    fd :size / 2
    rt 90
  ]
END

TO sierpinskiexample
  sierpinski 500 8
END

sierpinskiexample

Neat but a bit plain. We could use frag to create filled triangles, but we need to avoid z-fighting by adding a little bit of code to change the elevation of each ‘level’:

TO sierpinski :size :level
  if :level > 0 [

    pu setz 0 lower 0.1 * :level
    ;add above line to avoid z-fighting

    rt 30
    repeat [
      fd :size
      rt 120
    ]

    setfc :level
    ;set the fill color to the current 'level'
    frag
    ;create a filled triangle from the last three points (triangle)

    left 30
    sierpinski :size / 2 :level - 1
    rt 30
    fd :size / 2
    left 30
    sierpinski :size / 2 :level - 1
    rt 30
    back :size / 2
    left 30
    rt 90
    fd :size / 2
    left 90
    sierpinski :size / 2 :level - 1
    left 90
    fd :size / 2
    rt 90
  ]
END

sierpinskiexample

If you seperate the layers more, and use shard instead of frag…

Sierpinski’s Tree

Trees are also a lot of fun, with the potential for so many variations!

TO tree :s :a :frac :depth
  fd :s / 2
  if :s >= 1 [
    local "p
    local "h
    make "p pos
    make "h heading
    left :a
    tree :s * 2 / 3 :frac * :a :frac :depth + 1
    pu setpos :p pd
    seth :h + :a
    tree :s * 2 / 3 :frac * :a :frac :depth + 1
  ]
END

TO drawtree
  reset
  cs pu bk 250 pd 
  tree 350 25 1.1 4
END

Note that this takes quite some time to render!

tree 350 60 1.1 4

TO tree :s :a :frac :depth
  fd :s / 2   
  if :s >= 1 [
     setpc :s
     ;set the pen color to the current 'size'
     ;which is fractional number truncated to an integer for use by setpc
     local "p
     local "h
     make "p pos
     make "h heading
     left :a     
     tree :s * 2 / 3 :frac * :a :frac :depth + 1
     pu setpos :p pd     
     seth :h + :a
     tree :s * 2 / 3 :frac * :a :frac :depth + 1
   ] 
END

tree 350 180 1.1 4

setpc 12 - :s

tree 350 280 1 4

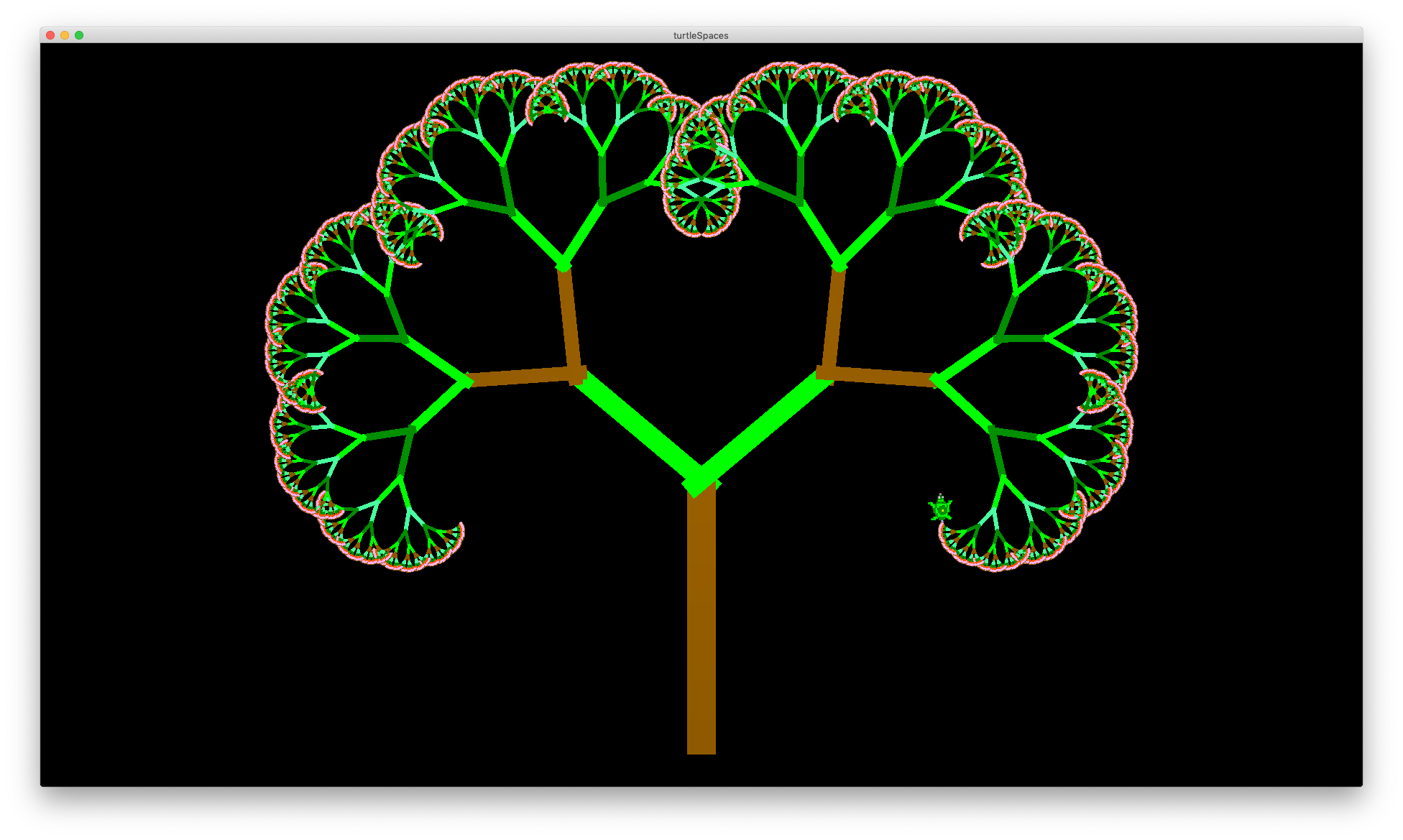
Play with tree’s parameters and the colors and see what you can come up with! Logo is all about exploration, tweaking and tinkering. By seeing how altering the parameters can change the end result, you can learn to better understand the underlying mathematics.

You can also change how the trees are rendered, for example using mark instead of forward and by setting the width of the mark using setmarkerwidth depending on the current ‘size’ of the segment being rendered:

TO tree :s :a :frac :depth
   penup
   setpc item (remainder int :s 7) [11 9 4 12 14 8 13]
   if pencolor = 0 [setpc 8]
   setmarkerwidth 1 + :s / 20
   bk :s / 20
   mark :s / 2
   if :s >= 1 [
      local "p
      local "h
      make "p pos
      make "h heading
      left :a
      tree :s * 2 / 3 :frac * :a :frac :depth + 1
      pu setpos :p pd
      seth :h + :a
      tree :s * 2 / 3 :frac * :a :frac :depth + 1
   ]
END

cs tree 300 50 0.88 4

Et voila!