Past and Future Turtles: The Evolution of the Logo Programming Language (Part 1)
When I was a young child, one of my best friends was a turtle.
Not a real turtle, although that would have been fun, but a virtual one. My turtle lived inside of an Apple II, an early 8-bit computer, at my elementary school.
When I first met her, my turtle, she didn’t do much. She just sat there. It didn’t take long for me to realize that in order to get her to do something, I would need to prompt her. To do this, there was a literal prompt on the screen, beckoning me to type something.
?
And so I typed FORWARD, thinking that this should, obviously, move the turtle forward.
NOT ENOUGH INPUTS TO FORWARD
Undeterred, I revised my input to FORWARD 10, just picking an arbitrary number. Although I was only six years old, I deduced that FORWARD needed a quantity, quantities were numbers and well, ten was a good start.
And hooray, the turtle moved! I was in love with my turtle from that moment on. I learned that she could also move BACK, and turn LEFT and RIGHT. I didn’t know what degrees were when I first met my turtle, but by the time I finished our first session together, I did!

Seymour Papert in 1971
That afternoon in 1981, I had learned some of a programming language called Logo. The father of Logo was a mathematician and philosopher named Seymour Papert. Interested in learning how to improve mathematics education in young children, in the early 1960s, he had studied under Jean Piaget, a Swiss psychologist who championed a philosophy of learning known as constructivism.
When children are given new information, for example, that a full turn is made up of 360 degrees, they are likely to only accept that information if they already have the underlying understanding required, such as that a turn can be divided in half, quarters and so on, down to 360ths. Or even the concept of a number as high as 360 can exist in the first place.
Otherwise, they are likely to either misinterpret the new information to fit their current understanding (“I only understand numbers as high as 100, and so they must mean 100”) or will simply ignore it, with a silent internal ‘syntax error’.
This can improve if a) the teacher explains numbers up to 360, b) the teacher explains division and then finally c) the teacher explains that when you spin around, you are making a circle (hold out your arm! The point of your finger draws a circle when you spin) and if you spin around halfway, you’re moving 180 degrees and so on.
This may still not be enough. If the child fails to understand a, b and / or c, they still won’t understand it.
However, if the child is able to actively explore these concepts in an environment that has some measure of feedback, the likelihood of their gaining understanding improves. For example, if the teacher suggests they turn randomly, and the teacher tells them how far they have turned each time they do it, they will soon learn that if they turn halfway, they have turned 180 degrees. They will learn that a full turn is 360 degrees. They will understand that the next number after 100 is 101, and hence the next number after 200 is 201. And so on.
This is what Papert learned under Piaget. But obviously, while desirable it’s not practical for each child to have an adult giving them feedback on everything they do until they understand it. The world just doesn’t (and probably will never have) a 1:1 student to teacher ratio. This was a problem Piaget and Papert simply couldn’t surmount.
But in the early 1960s, a new technology was emerging, one that Papert realized could remove his roadblock – the computer.
Computers did not tire, they did not lose patience. Although at that time large and small in number, it was not hard for Papert to see the future, a future where schools were full of terminals connected to computers, one for each child, with which the students could explore ‘mathland’, a simple environment where mathematical concepts could be demonstrated through trial and error. The more input students provided, and the more output they absorbed, the sooner they would grasp concepts. Computers seemed a perfect fit for the task of educating children using constructivist principles.
 In 1961, Papert had met an American, Marvin Minsky, at a conference in England. They presented papers that were surprisingly similar, and connected as a result. So, powered by his idea of using computers to teach children, in 1964, Papert went to the US, and joined Minskey’s Artificial Intelligence Group, a team of researchers at the Massachusetts Institute of Technology (MIT).
In 1961, Papert had met an American, Marvin Minsky, at a conference in England. They presented papers that were surprisingly similar, and connected as a result. So, powered by his idea of using computers to teach children, in 1964, Papert went to the US, and joined Minskey’s Artificial Intelligence Group, a team of researchers at the Massachusetts Institute of Technology (MIT).
Papert was impressed with the technology-centric culture at MIT, and attitude that everyone had the potential to learn anything they wanted to, a position Papert shared. The students under Minsky and Papert had free rein to work on whatever they wanted, encouraging experimentation and the practical testing of even the most wild theories. Papert saw how his students, when encouraged, would learn great amounts of knowledge on their own, and collaborate with others to get past roadblocks they encountered in their pursuits. At MIT these students were known as ‘hackers’.
One of these hackers, Daniel Bobrow, graduated and got a job at a research and development (R&D) firm called Bolt, Beranek and Newman. In the mid-1960s they had started exploring computer technologies, and their potential. Bobrow became head of their new Artificial Intelligence group. There, he met Wally Feurzeig, who was leading BBN’s education group. The space race had encouraged the US government to find ways of improving math education in schools, and BBN was hoping to find a solution. They had already developed ‘time-sharing’ technology which allowed a mainframe computer to be used by many people at the same time, they just needed software to run on it that children could use to learn.
Bobrow brought in Papert and introduced him to Feurzeig, and the three discussed the idea of developing a computing language for children, Papert’s Mathland. Around that time, BBN had a visitor who demonstrated a new programming language called BASIC. Rather than using memory addresses, BASIC used line numbers to track execution, and named variables that transparently linked to memory addresses. These abstractions made it much easier for non-computer scientists to create computer programs.
BBN’s researchers created a version of BASIC they called Telcomp, which Feurzeig modified to include strings, and called Stringcomp. BBN trialed Stringcomp (using teletypes, typewriters connected to a remote computer) in eight elementary and junior high-school classrooms in 1966. That year, Minsky’s assistant at MIT, Cynthia Solomon, joined Feurzeig’s team at MIT.

Seymour Papert at Muzzey Junior High School in 1966
After Papert visited these classrooms and saw the interaction between children and Stringcomp, he became convinced that BASIC was not the answer, and that a new language would need to be written, one more suited to learning.
Importantly, the new language would need to more adequately demonstrate how the computer came to its conclusions. Papert felt that due to computers’ requirements for literal instruction, children would be able to see how the computer ‘thought’ and realize that was how they themselves also thought, helping them break down problems into smaller elements the way a computer would when it solved them. Thus, the new language would serve a dual purpose, both teaching mathematics, and how mathematics are solved.
BASIC was too monolithic in its command-based structure, and those ‘smaller parts’ could not be shown to its users, happening behind the scenes and out of sight.
And so, the new language would both need to be able to accomplish what one could accomplish in BASIC, while doing so using smaller steps that could be inspected by novice programmers. But to avoid needless and redundant repetition of code, these steps would need to be able to be reused. Because of the philosophy behind it, Wally Feurzeig christened the new language ‘Logo’, derived from Logos, the greek word for ‘thought’.
Minsky, Papert and Solomon had a number of discussions about how Logo would work. Solomon had learned some of the Lisp programming language (a language where all code and data are written in the form of expressions and lists, the name Lisp short for LISt Processing) while Minsky’s assistant, and she appreciated its power for manipulating English language strings, which she recognized could be used as a method by which students could observe the effects of computer code on recognizable data, or data that they created themselves.
It also probably didn’t hurt that Lisp had been invented by the same BBN employee (and MIT alumnus) that had developed its time-sharing system. And so, it was decided that the new language would be a variant of Lisp.
However, Lisp had some drawbacks in terms of its use with younger coders. It had an extreme reliance on structure, using an intricate array of parentheses which often led to errors that were hard to resolve (leading to nicknames Lost in Stupid Brackets and Lots of Irritating Superfluous Parentheses). Its interpreter was also bulky, and not interactive, like BASIC.
In designing Logo, Papert, Minsky and Solomon took the expression, list and string elements of Lisp, removing much of the need for brackets by making assumptions about syntax parsing and inputs, and later allowing for the ‘stacking’ of what they called ‘primitives’ (functions which may or may not resolve to a value) on a single line, such that you could type:
PRINT SUM 4 4
and the computer would output 8, or:
TYPE 1 TYPE 2 TYPE 3
and the computer would output 123.
Lists allowed for the string manipulation Solomon had been hoping for:
(PRINT PICK [RED GREEN BLUE] PICK [DOG CAT BOAT])
BLUE BOAT
RED DOG
GREEN CAT
etc.
Logo was a lot more BASIC-like in its syntax and usage, while allowing for many features BASIC did not, such as the ability to create ‘procedures’, lists of primitives that could be named, and executed just like any other primitive, such as:
TO BOX
REPEAT 4 [
FORWARD 10
RIGHT 90
]
END
which could be executed simply by typing:
BOX
but even better:
TO POLY :SIDES :SIZE
REPEAT :SIDES [
FORWARD :SIZE
RIGHT 360 / :SIDES
]
END
the colon indicating a variable or container for storing a value.
POLY 4 10
would re-create our box, but the user could provide any desired values, like SUM. This satisfied Papert’s need to have both the ability to demonstrate computer problem-solving in smaller chunks, while also allowing for the reuse of code. Students could create the BOX or POLY procedures themselves, then use them in other procedures. A picture would form in their minds of the hierarchy of execution, and they would understand better how the computer, and they themselves, thought.
Except that we are getting ahead of ourselves with BOX and POLY, because in the beginning Logo did not have a turtle! When Logo was initially trialled in a seventh-grade classroom (in 1968 at Muzzey Junior High School in Lexington, Massachusetts), students were using the same teletypes the Stringcomp trial had used, and they used Logo to manipulate lists and strings rather than a turtle. Which worked quite well to engage students who were strong in English, but failed to engage those who were not.

Cynthia Solomon (left) and Seymour Papert (right) at Muzzey Junior High in 1966
Also, on the teletype math was still just numbers, regardless of the more elegant way Logo could break down mathematical equations. Kids who didn’t ‘get’ numbers still didn’t get numbers! Papert craved some sort of graphical representation, but the technology at the time strongly precluded that. And so, towards the end of the trial, he had the idea of creating a physical robot, one that could move about on the floor, and draw out graphical representations of mathematic output.

 Papert and Solomon left BBN and headed back to MIT, where they formed the Logo Group. In England, two robots had been developed that could wander about a space, their inventor dubbing them ‘tortoises’. The Logo Group developed their own robots, calling them turtles. Having access to expensive display hardware, they also developed a virtual turtle, one that lived on the computer screen.
Papert and Solomon left BBN and headed back to MIT, where they formed the Logo Group. In England, two robots had been developed that could wander about a space, their inventor dubbing them ‘tortoises’. The Logo Group developed their own robots, calling them turtles. Having access to expensive display hardware, they also developed a virtual turtle, one that lived on the computer screen.
 They added primitives to Logo to control the turtle: FORWARD, BACK LEFT, RIGHT. And they discovered that Papert had been right – children took to the turtle, the turtle allowing Logo users to have a perspective inside the computer, that of the turtle, rather than depending on an understanding of abstract concepts of code paths or numbers. The procedural structure of Logo meant the turtle could be ‘taught’: taught how to draw a square, taught how to draw a polygon, creating them inside of its environment, interacting it and shaping it like a child scrawling on the wall of their bedroom.
They added primitives to Logo to control the turtle: FORWARD, BACK LEFT, RIGHT. And they discovered that Papert had been right – children took to the turtle, the turtle allowing Logo users to have a perspective inside the computer, that of the turtle, rather than depending on an understanding of abstract concepts of code paths or numbers. The procedural structure of Logo meant the turtle could be ‘taught’: taught how to draw a square, taught how to draw a polygon, creating them inside of its environment, interacting it and shaping it like a child scrawling on the wall of their bedroom.
 The turtle allowed for an empathetic bond to form between it and the child, giving the child a dual sense of accomplishment when the turtle succeeded at what the child told it to do – both because the child correctly instructed the turtle, and the turtle successfully carried out those instructions, the result of the latter the evidence of the former. The child could also ‘think like the turtle’ when developing procedures and debugging, moving about the room as the turtle would, figuring out roughly what they needed the turtle to do, and then refining their program as needed.
The turtle allowed for an empathetic bond to form between it and the child, giving the child a dual sense of accomplishment when the turtle succeeded at what the child told it to do – both because the child correctly instructed the turtle, and the turtle successfully carried out those instructions, the result of the latter the evidence of the former. The child could also ‘think like the turtle’ when developing procedures and debugging, moving about the room as the turtle would, figuring out roughly what they needed the turtle to do, and then refining their program as needed.

An early Logo video display
While Logo’s string and list facilities are impressive, it is fair to say the turtle made Logo. Both the physical and virtual turtles were used by fifth graders at the Bridge School in Lexington in a trial during 1970 and 1971. But both robots and video terminals were expensive in the 1970s, and schools hadn’t widely adopted computer terminals; as such, there was no widespread use of Logo in the 1970s.
However, the emergence of the home computer market in the late 1970s provided an opportunity for Logo to reach a wider segment of the population. In 1980, Minskey, Papert, Solomon and two Canadians founded Logo Computer Systems Inc. (LCSI) and in 1981 they published a version of Logo for the Apple II computer, which I booted up and met Seymour, Cynthia and Marvin’s turtle for the first time.
They would have been very happy I learned about degrees (and other things) from their turtle!
But where did Logo go from there? Carry on to Past and Future Turtles: Logo’s Adventures in Academia (Part 2)
And don’t forget to try our weblogo… or read the Hacker News discussion!
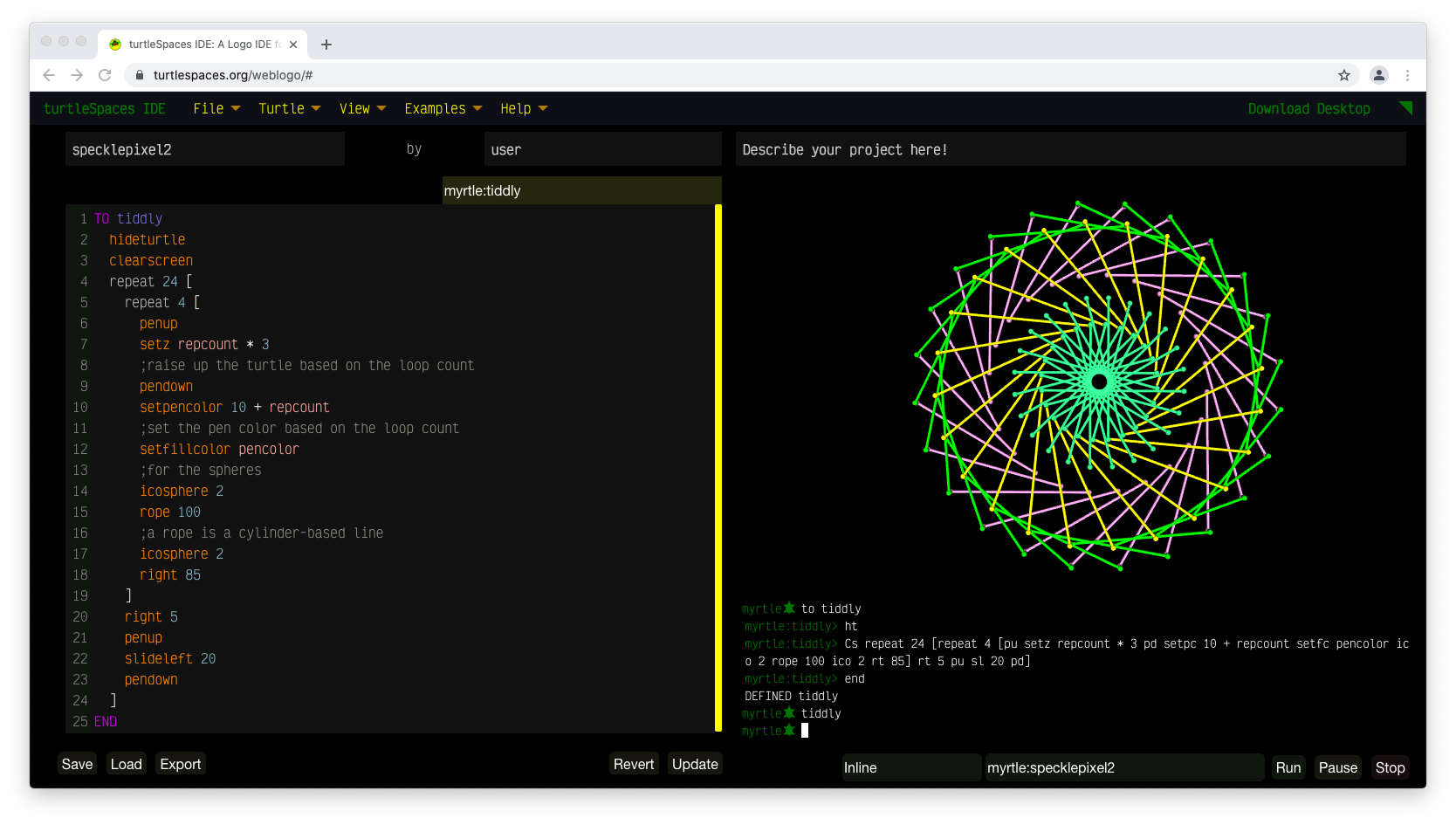


 You can change the color of the star using the SETFILLCOLOR primitive, or set a random fill color with RANDFC.
You can change the color of the star using the SETFILLCOLOR primitive, or set a random fill color with RANDFC.