Sierpinski’s Gasket
These routines use recursion (they repeatedly call themselves) to realise different Sierpinski algorithms. Logo’s recursion capabilities and relational turtle make it excellent for the task of rendering these algorithms! They’re also very pretty.
TO half_s :size :level
if :level = 0 [fd :size stop]
half_s :size :level - 1
lt 45 fd :size * sqrt 2 lt 45
half_s :size :level - 1
rt 90 fd :size rt 90
half_s :size :level - 1
lt 45 fd :size * sqrt 2 lt 45
half_s :size :level - 1
END
TO sierpinski :size :level
repeat 2 [
half_s :size :level
rt 90 fd :size rt 90
]
END
TO sierp
cs pu back 180 pd sierpinski 3 5
END
sierp

Instead of drawing lines, we can construct triangles out of ‘pins’ dropped at appropriate points:
TO half_s :size :level
penup
if :level = 0 [fd :size stop]
pin
;pin marks a point for use with pinfrag
half_s :size :level - 1
lt 45 fd :size * sqrt 2 lt 45
half_s :size :level - 1
rt 90 fd :size rt 90
half_s :size :level - 1
lt 45 fd :size * sqrt 2 lt 45
half_s :size :level - 1
pinfrag
;creates a triangle out of the last three 'pins'
END
sierp

We could drop twice as many pins and then select a color for each ‘frag’ (fragment) triangle from a list:
TO half_s :size :level
pu
if :level = 0 [fd :size stop]
pin
;drop pin
half_s :size :level - 1
lt 45 fd :size * sqrt 2 lt 45
half_s :size :level - 1
pin
;drop another pin
rt 90 fd :size rt 90
half_s :size :level - 1
lt 45 fd :size * sqrt 2 lt 45
half_s :size :level - 1
setfc item :level [9 8 1 13] pinfrag
;pick a color from a list based on the current level and create the fragment
END
sierp

Sierpinski’s Triangle
It’s triangles all the way down!
TO sierpinski :size :level
if :level > 0 [
rt 30
repeat 3 [
fd :size
rt 120
]
left 30
sierpinski :size / 2 :level - 1
rt 30
fd :size / 2
left 30
sierpinski :size / 2 :level - 1
rt 30
back :size / 2
left 30
rt 90
fd :size / 2
left 90
sierpinski :size / 2 :level - 1
left 90
fd :size / 2
rt 90
]
END
TO sierpinskiexample
sierpinski 500 8
END
sierpinskiexample

Neat but a bit plain. We could use frag to create filled triangles, but we need to avoid z-fighting by adding a little bit of code to change the elevation of each ‘level’:
TO sierpinski :size :level
if :level > 0 [
pu setz 0 lower 0.1 * :level
;add above line to avoid z-fighting
rt 30
repeat [
fd :size
rt 120
]
setfc :level
;set the fill color to the current 'level'
frag
;create a filled triangle from the last three points (triangle)
left 30
sierpinski :size / 2 :level - 1
rt 30
fd :size / 2
left 30
sierpinski :size / 2 :level - 1
rt 30
back :size / 2
left 30
rt 90
fd :size / 2
left 90
sierpinski :size / 2 :level - 1
left 90
fd :size / 2
rt 90
]
END
sierpinskiexample

If you seperate the layers more, and use shard instead of frag…


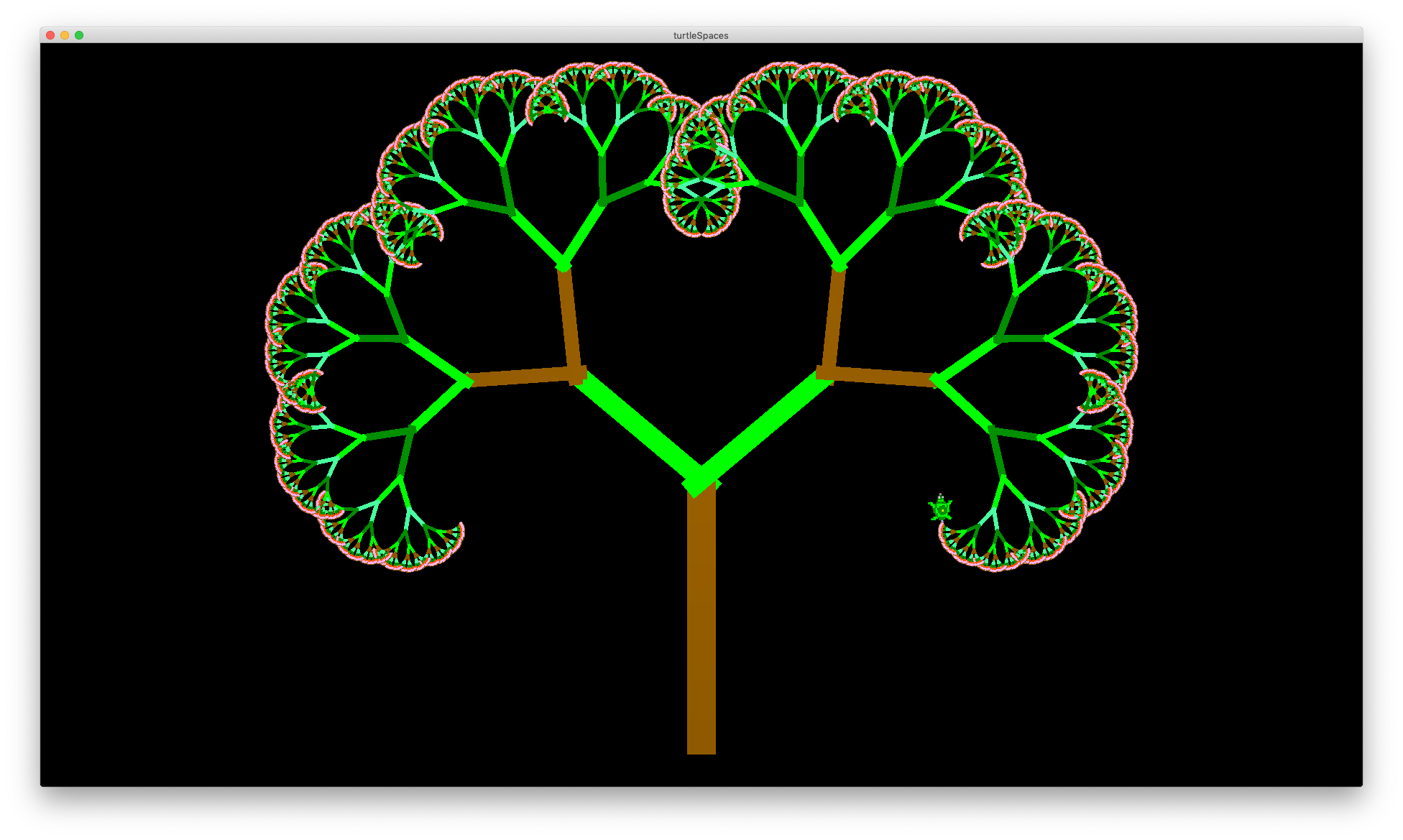
Sierpinski’s Tree
Trees are also a lot of fun, with the potential for so many variations!
TO tree :s :a :frac :depth
fd :s / 2
if :s >= 1 [
local "p
local "h
make "p pos
make "h heading
left :a
tree :s * 2 / 3 :frac * :a :frac :depth + 1
pu setpos :p pd
seth :h + :a
tree :s * 2 / 3 :frac * :a :frac :depth + 1
]
END
TO drawtree
reset
cs pu bk 250 pd
tree 350 25 1.1 4
END

Note that this takes quite some time to render!
tree 350 60 1.1 4

TO tree :s :a :frac :depth
fd :s / 2
if :s >= 1 [
setpc :s
;set the pen color to the current 'size'
;which is fractional number truncated to an integer for use by setpc
local "p
local "h
make "p pos
make "h heading
left :a
tree :s * 2 / 3 :frac * :a :frac :depth + 1
pu setpos :p pd
seth :h + :a
tree :s * 2 / 3 :frac * :a :frac :depth + 1
]
END
tree 350 180 1.1 4


setpc 12 - :s
tree 350 280 1 4


Play with tree’s parameters and the colors and see what you can come up with! Logo is all about exploration, tweaking and tinkering. By seeing how altering the parameters can change the end result, you can learn to better understand the underlying mathematics.
You can also change how the trees are rendered, for example using mark instead of forward and by setting the width of the mark using setmarkerwidth depending on the current ‘size’ of the segment being rendered:
TO tree :s :a :frac :depth
penup
setpc item (remainder int :s 7) [11 9 4 12 14 8 13]
if pencolor = 0 [setpc 8]
setmarkerwidth 1 + :s / 20
bk :s / 20
mark :s / 2
if :s >= 1 [
local "p
local "h
make "p pos
make "h heading
left :a
tree :s * 2 / 3 :frac * :a :frac :depth + 1
pu setpos :p pd
seth :h + :a
tree :s * 2 / 3 :frac * :a :frac :depth + 1
]
END
cs tree 300 50 0.88 4

Et voila!
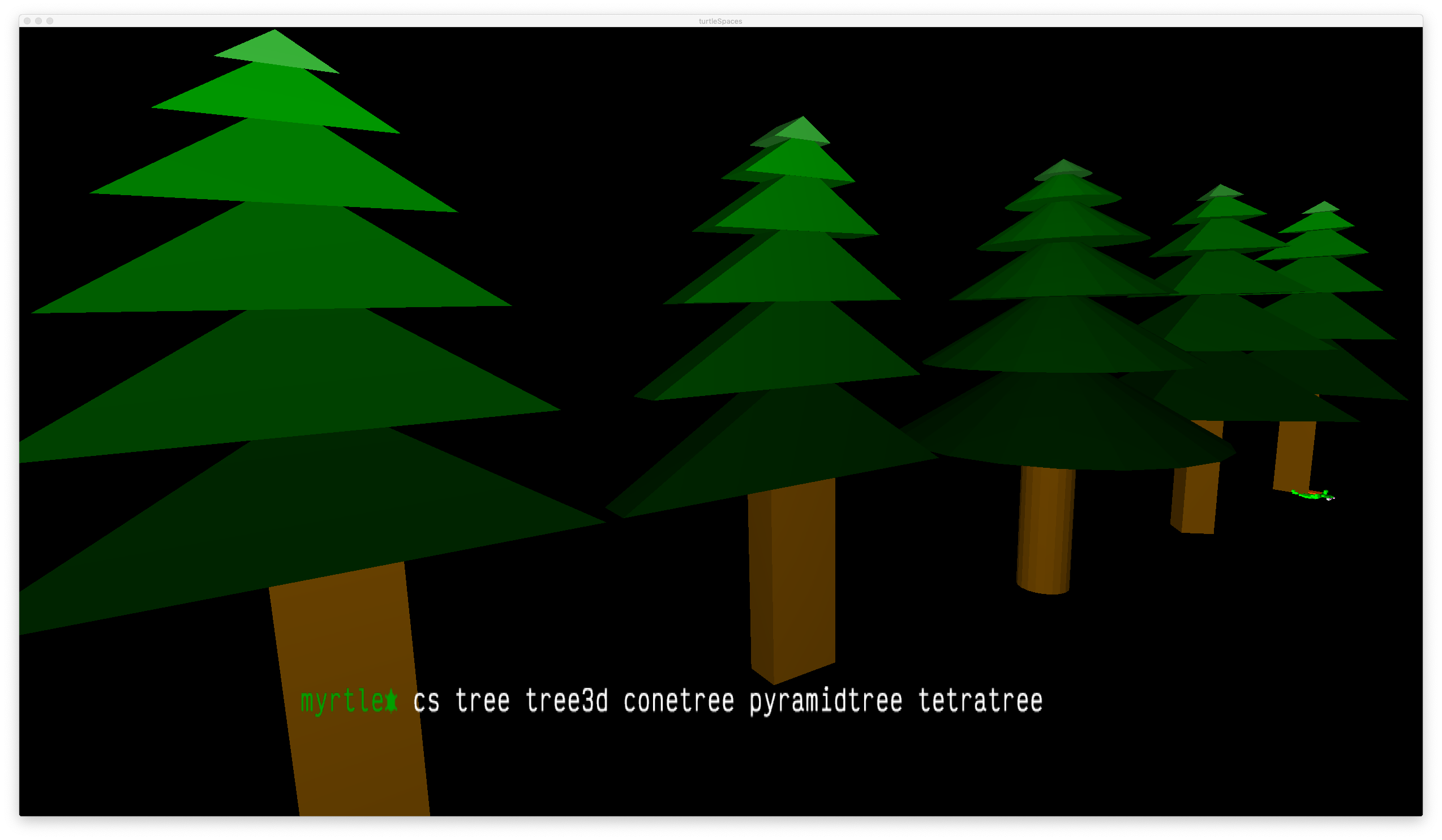
TO tree clearscreen penup setpos [0 80] setfillcolor 4 repeat 6 [ setfillshade -6 + 3 * repcount ;repcount returns the current iteration back 4 * repcount fiso 8 * repcount 5 * repcount ;fiso = filled iso triangle lower 0.1 ] setfillcolor 8 setfillshade 5 back 50 slideleft 10 quad 20 50 ;trunk END
TO tree3d cs pu setpos [0 80] ;cs = clearscreen ;pu = penup setfc 4 ;setfc = setfillcolor repeat 6 [ setfs -6 + 3 * repcount ;setfs = setfillshade bk 4 * repcount ;bk = back tent 8 * repcount 5 * repcount 10 lo 0.1 ;lo = lower ] setfc 8 setfs 5 bk 50 sl 10 ;sl = slideleft voxeloid 20 50 10 ;voxeloids are stretched cubes END
TO conetree cs pu setpos [0 80] setfc 4 up 90 repeat 6 [ setfs -6 + 3 * repcount ra 4 * repcount cone 8 * repcount 5 * repcount 20 ] setfc 8 setfs 5 ra 50 cylinder 8 50 20 END
TO pyramidtree cs pu setpos [0 80] setfc 4 up 90 repeat 6 [ setfs -6 + 3 * repcount ra 4 * repcount cone 8 * repcount 5 * repcount 4 ;while there is also a pyramid primitive, you can ;also create a pyramid by creating a 4-sided cone ] setfc 8 setfs 5 ra 50 cylinder 8 50 4 END
TO tetratree cs pu setpos [0 80] setfc 4 up 90 repeat 6 [setfs -6 + 3 * repcount ra 4 * repcount cone 8 * repcount 5 * repcount 3] setfc 8 setfs 5 ra 50 cylinder 8 50 3 END