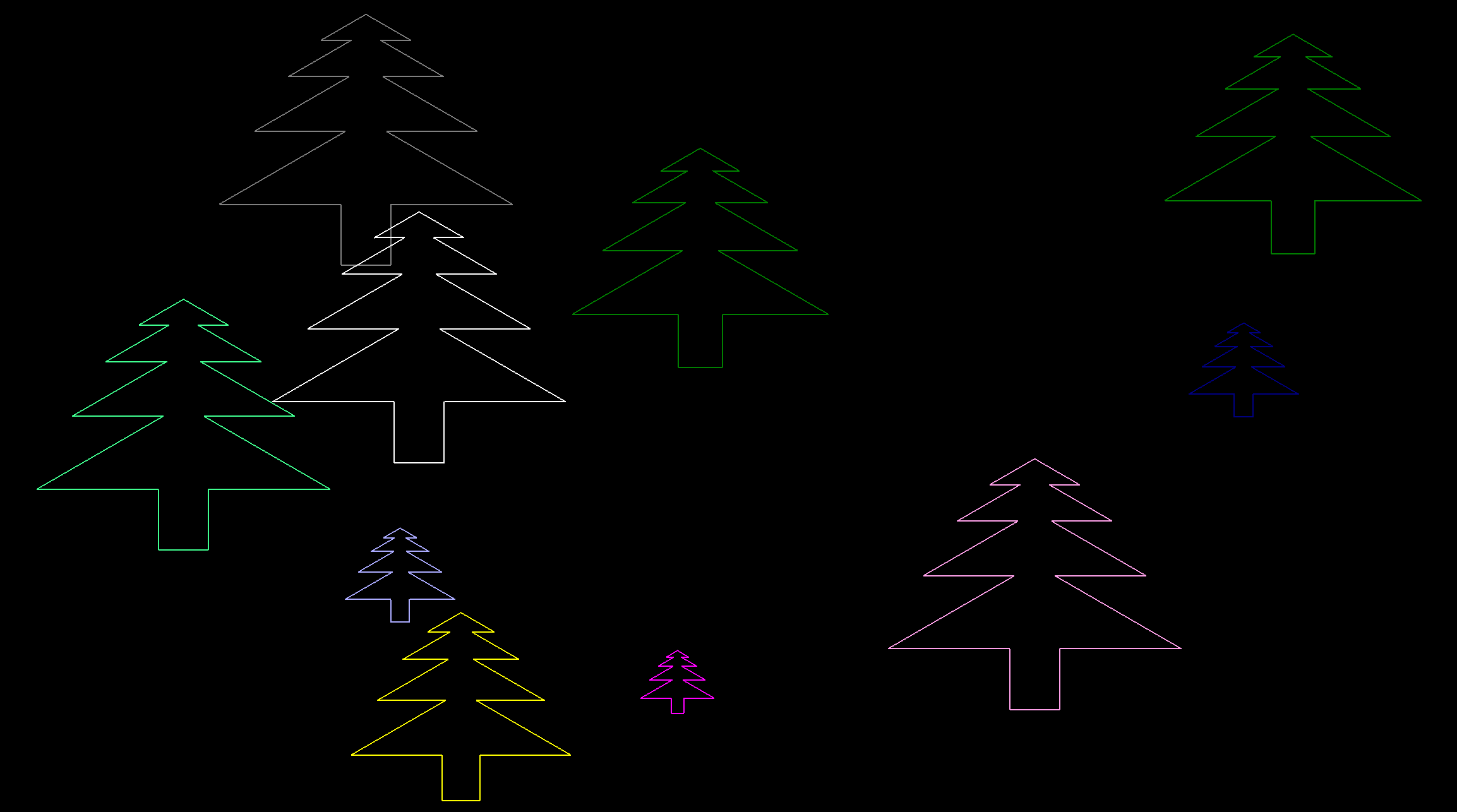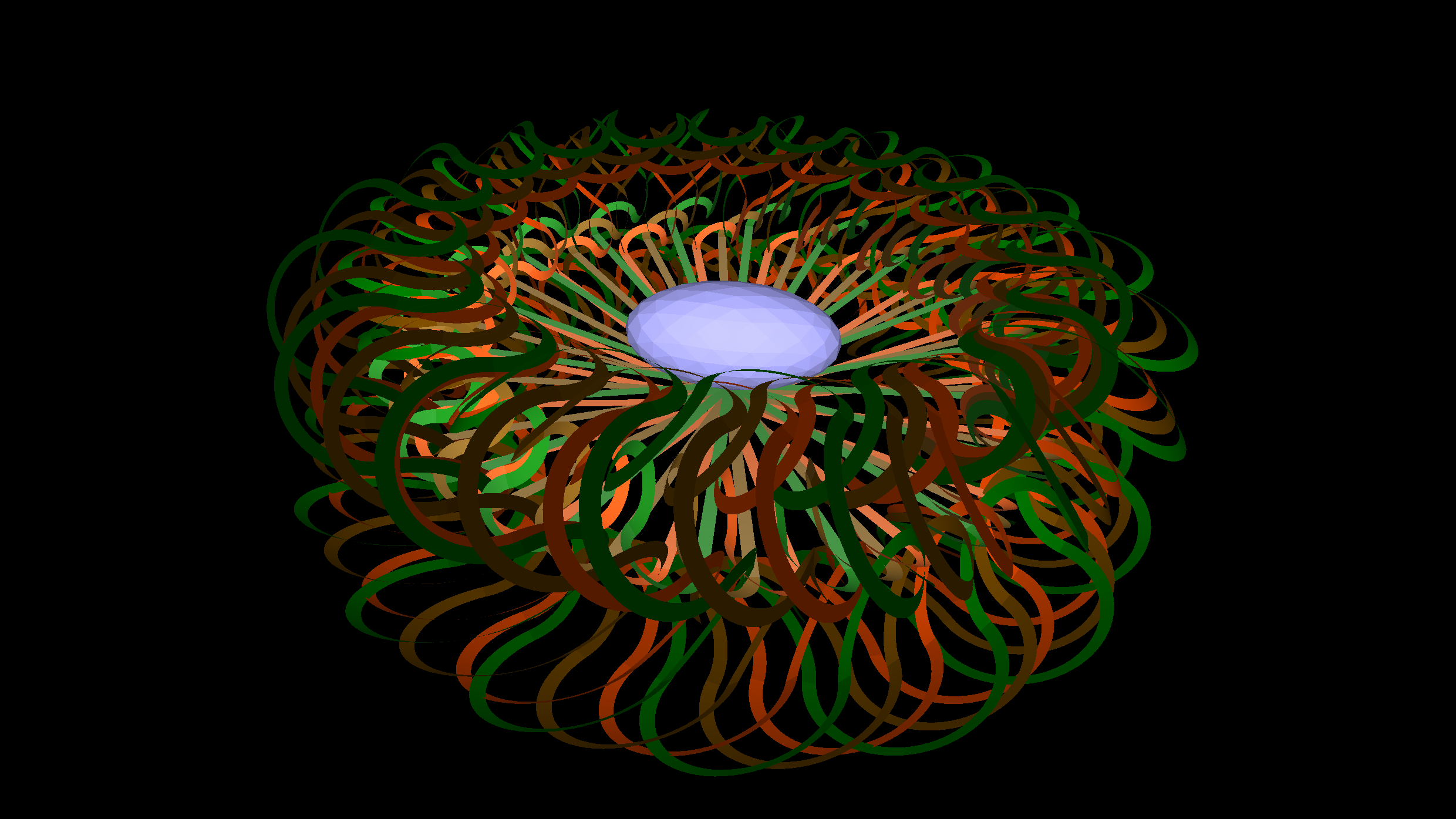
Examples: Turtle Art
Logo is great for creating art! And 3D Logo makes it even better.
Many of these Logo artworks were inspired by examples created by Seymour Papert’s daughter Artemis Papert using the two-dimensional block-based TurtleArt application developed by LCSI Logo developer Brian Silverman. We’re grateful for both of their efforts in advancing Logo over the past several decades!

TO adobo
reset setpenwidth 5 definecolor 16 [0 0 0]
setpc 16 setbg 1 setbs 12 pu
repeat 9 [
repeat 10 [
setpos {-120 + 20 * repcount -120 + 20 * repabove 1}
setz -2 + 0.01 * random 400
setfc pick [8 9 13]
setfs -13 + random 10
setheading -5 + random 11
square 40 box 40
]
]
END

TO brush
reset setbg 8
setpenwidth 5 setbs 11
repeat 300 [
setpc pick [1 8 9 11]
setps -10 + random 20
pu
setpos {-200 + random 400 -100 + random 200}
rt random 360 pd
repeat 20 + random 50 [
make "stroke 30 + random 150
fd :stroke rt -0.5 + 0.1 * random 10
bk :stroke + random 2 lt -0.5 + 0.1 * random 10
]
ra 0.01
]
END




TO bundles
reset randbg
repeat 40 [
pu setpos {-200 + random 400 -100 + random 200}
setpenwidth 4 pd
lt random 360
make "head heading
repeat 2 [
randpc
repeat 90 [
make "stroke 50 + random 5
setps -10 + random 20
fd :stroke
bk 2 * :stroke
fd :stroke
rt 0.1 * random 20
up -2 + (0.1 * random 40)]
setheading :head
]
]
END



TO burst
reset pu
make "colors {yellow orange red magenta blue}
repeat 5 [
setpc item repcount :colors
setmarkerwidth repcount
make "count repcount
repeat 50 [
rt random 360 mark :count * (20 + random 10)
setpos [0 0]] lo repcount
]
END

TO caduceus
reset setpenwidth 5 pu
repeat 4 [
setpc item repcount [13 9 1 8]
ra repcount * 2
bk 120 pd
repeat 100 [
fd 1.4 + 0.1 * repabove 1
rt 7.5 * sin 270 + 10 * repcount
]
repeat 75 [
fd 2.5 + 0.5 * repabove 1
lt 0.5 * repcount
]
pu home rr 180 * repcount
]
END

TO cards
reset pu
repeat 1000 [
setpos {-200 + random 400 -100 + random 200}
rt random 360
make "sizex 10 + random 20
make "sizey 10 + random 20
setfc 2 setfs 13
quad :sizex + 2 :sizey + 2
sr 1 fd 1 ra 0.01
setfc pick [2 3 7 14]
setfs -5 + random 10
quad :sizex :sizey
ra 0.01
]
END


TO citylights
reset pu setbg 2 setbs 10
repeat 200 [
setpos {-200 + random 400 -100 + random 200}
rt random 360 make "size 20 + random 50
setfc pick [1 9 13 7] lo 0.01
until :size = 0 [
randfs spot 0.05 * :size
fd 5 lo 0.01 dec "size
]
]
END


TO dotcube
cs seticosphereiterations 1 pu
repeat 9 [
repeat 9 [
repeat 9 [
setposition {-100 + 20 * repabove 2 -100 + 20 * repabove 1 -100 + 20 * repcount}
setfc repabove 1 setfs repcount ico 2
]
]
]
END

TO dotspiral
Reset setbg 13 setfc 9 cs
repeat 1400 [
pu fd repcount / 10
spot repcount / 250
rt 35
]
END


TO fireworks
cs setpenwidth 5
repeat 60 [
pu home
rt random 360
randpc pd
fd 30 + random 50
repeat 50 [
run pick [[pu][pd]]
fd 2]
]
END

TO fish
reset wrap
setbounds [-180 -120 180 120]
setbg 1 setbs 12
pu setpos [-170 75]
repeat 12 [
setpenwidth 4 rt 44.5
repeat 10 [
sl 1
repeat 3 [
setpc item repcount [13 1 13]
if repcount = 2 [ra 0.2]
if repcount = 3 [lo 0.2]
pd fd 50 pu bk 50 pu sr 1
]
sl 2 rt 10
]
setfc 1 ico 1 st
lt 54.5 sr 13 fd 60
lt 90
]
END

TO gaia
reset setbg 2 setpenwidth 5 setpc 1
repeat 5 [
setpc item repcount [8 1 9 13 15]
setorigin {0 0 2 * repcount}
repeat 20 [
pu home pd rt repcount * 18
repeat 80 [
fd 0.9 + ((repabove 2) * 0.1)
rt 8 * sin (repcount * 8)
]
lt 7.5
repeat 5 [
fd 20 pu bk 20 rt 15 pd
]
]
]
END


TO gradient
cs pu
repeat 30 [
setfs -15 + repcount quad repcount 200 lo 0.01 sl 0.5
]
END

TO gridart
reset
randbg
randfc
pu
setpos [-210 113]
repeat 31 [
for [i 1 57] [
spot 3.5 * sin ((:i + repcount) * 2)
sr 7.5
]
sl 57 * 7.5
bk 7.5
]
END

TO gridartico
cs
seticosphereiterations 1
pu
setpos [-210 113]
repeat 31 [
for [i 1 57] [
ico 3.5 * sin ((:i + repcount) * 2)
sr 7.5
]
sl 57 * 7.5
bk 7.5
]
END

TO gridartshade
reset randbg randfc pu
setpos [-210 113]
repeat 31 [
for [i 1 57] [
setfs int (10 * (sin ((:i + repcount) * 2)))
spot 3.5
sr 7.5
]
sl 57 * 7.5 bk 7.5
]
END

TO gridartwave :size
cs
seticosphereiterations 1
pu
setpos [-210 113]
repeat 31 [
for [i 1 57] [
make "sin 3.5 * sin ((:i + repcount) * 2)
ra :size * :sin
ico :sin
lo :size * :sin
sr 7.5]
sl 57 * 7.5
bk 7.5
]
END

TO guessing
Reset setspeed 5 setbg 9 setbs 3 setpenwidth 5
repeat 8 [
pu home ra repcount rt repcount * 45 pd
repeat 22 [
if repcount < 4 [
setpc 8 setps 9 - (3 * repcount)] [
setpc 13 setps (penshade - 1) + random 3
]
repeat 360 [fd 1 - (0.015 * repabove 1) rt 1]
pu sr 0.02 pd
]
]
END



TO heat
cs pu
repeat 10 [
setfc pick [1 9 13]
setpos {-170 + (repcount * 30) -120}
up 90
repeat 80 [
cylinder 0.1 * repcount 1.6 10
sr sin (repcount * 10)
lo 1.5
]
repeat 80 [
cylinder 0.1 * (80 - repcount) 1.6 10
sr sin ((80 + repcount) * 10)
lo 1.5
]
dn 90
]
END

TO heat2
cs pu
repeat 10 [
setfc pick [1 9 13]
setpos {-170 + (repcount * 30) -120}
up 90
repeat 80 [
cylinder 0.1 * repcount 1.6 10
sr sin (repcount * 10)
lo 1.5
]
repeat 80 [
cylinder 0.1 * (80 - repcount) 1.6 10
sr sin ((80 + repcount) * 10)
lo 1.5
]
dn 90 rr 180
]
END

TO hedgehog
reset setfc 1 pu ra 1 spot 20 setpc 13
repeat 36 [
home dropanchor tether pullout 18
orbitleft repcount * 10 rt 225
setmarkerwidth 0.1 * random 20
mark 30 + random 80
]
END

TO funnybird :col1 :col2
rl 90 setfc :col1 icospheroid 20 0.5
pu rr 90 fd 5 sr 12 lt 30
cylindroidarc 10 15 20 30 10 0.3
fd 10 sr 15 ra 2
setfc :col2 ico 3 lo 3.5 ico 3 ra 1.75
bk 10 dn 90 lt 90
domoid 10 8 20 0.3 fd 30 sl 7 rt 90
icospheroid 8 2 fd 14
icospheroid 8 2 bk 7 rr 30 rr 10 up 10
cylinder 2 35 20 lo 40 rr 180 lt 90 dn 10
domoid 7 10 10 0.5 oval 3.5 7 up 10 rt 90
rl 180 ra 35 dn 20 rl 20
cylinder 2 35 20 lo 40 rr 180 lt 90 up 10
domoid 7 10 10 0.5 oval 3.5 7
END
TO hiding
reset setpenwidth 5 pu
sl 30 funnybird 1 9 home
ra 20 rr 180 sl 30 up 10
funnybird 13 8 rl 180 fd 20
sr 20 spot 100 sl 40 up 90
rl 90 sl 60 pd setpc 13
pushturtle
repeat 50 [
popturtle
pushturtle
pu sr repcount * 2
pd lt -10 + random 30
setpc pick [8 9 13]
setfs -10 + random 20
raise -2 + random 6
repeat 70 + random 30 [fd 1 rt 0.7]
]
ht
END



TO icicles
reset pu up 90
repeat 20 [
setpos {-210 + (20 * repcount) 115}
make "size 20 + random 15 randfc
repeat :size [
cylinder 0.2 * (:size - repcount) 0.6 + (:size / 5) 20
ra 0.5 + (:size / 5)
]
]
END

TO moon
reset lt 120
repeat 180 [fd 1 rt 1]
rt 150
repeat 180 [fd 0.774 lt 0.676]
pu fd 30 pd
repeat 3 [
repeat 5 [
fd 20 bk 40 fd 20 rt 36
]
pu rt 180 sl 40 fd 40 pd
]
ht
END

TO needles
reset
repeat 5 [
repeat 10 [
pu setpos {-240 + 80 * repabove 1 126 - repcount * 23}
pushturtle rr 90 up -15 + random 30 randfc
cylinder 1 30 10 rr 180 cylinder 1 30 10 popturtle
]
]
END


TO nest
reset setspeed 1
repeat 3 [
setpc item repcount [9 8 4]
repeat 18 [
pu home raise 2 * repabove 1
rt 7 * repabove 1 rt repcount * 20
setps -5 up 10 pd
mark 50 + 2 * repabove 1
repeat 4 [
setps penshade + 2
repeat 90 [
pu bk 0.1 pd mark 0.2 + 0.1 * repabove 1
rt 2 up 1
]
setpenshade penshade + 1
repeat 90 [
pu bk 0.1 pd
mark 0.2 + 0.1 * repabove 1
lt 2 up 1
]
]
]
]
setfc 7 pu home ra 17 icospheroid 10 2 ht
END



TO notnot
reset pu sl 10 lt 40 setpc 15 setbg 1
setmarkerwidth 10 repeat 360 [
mark 1.1 bk 0.1 lt 1
]
lt 90 mark 115 home sr 90 fd 25 rt 40
repeat 360 [
mark 0.8 bk 0.1 lt 1
]
lt 90 mark 80
END


TO orangepeel
reset setpenwidth 8 setbs 3
setbg 13 setpc 9 setps 0
repeat 5 [
pu home
setpos {-240 + repcount * 50 113}
rt 100
repeat 10 [
sr 1.5 fd 1 pd setps -5 + repcount
repeat 100 [
if divisorp 10 repcount [
setps penshade + 1
]
fd 2.75 rt repcount
] lt 10
]
]
END

TO patio
cs pu setpos [-87.5 85] setfc 13
repeat 5 [
repeat 6 [
setfillshade -10 + random 21
make "offset random 10
lt 50 - :offset
polyspot 20 4
rt 50 - :offset
sr 35
]
sl 210 bk 35
]
END

TO peaks
reset ht pu bk 125 setbg 2
repeat 3 [
setfs 0 setfc 13
fiso 100 250
setfc 7 setfs repcount * 3
ra 0.1
fiso 75 200
sl 120 lo 50 bk 30
]
home bk 125 sr 120 lo 50 bk 30
repeat 2 [
setfc 13 setfs 0 fiso 100 250
setfs 3 + repcount * 3
setfc 7 ra 0.1 fiso 75 200
sr 120 lo 50 bk 30
]
setpenwidth 5 home setpos [140 80]
setpc 13
repeat 36 [
pd fd 35 pu bk 35 rt 10
]
END


TO pinwheel
reset twosided
pu setbg 2
setfc 14 setpc 7
repeat 2 [
setpc item repcount [7 11]
setfc item repcount [14 13]
pu home rt repcount * 45
bk 10
repeat 100 [
fd 40 + repcount * 1.2
lt 90 fd 10 lt 92 fd 10
frag lt 90
]
]
END

TO postits
reset pu
repeat 10 [
repeat 10 [
setpos {-120 + 20 * repcount -120 + 20 * repabove 1}
randfc
setheading -5 + random 11
square 20 ra 0.1
]
]
END


TO rainbow
reset setpenwidth 10 pu sl 225 bk 125 lt 10 pd
repeat 500 [
foreach "col {red orange yellow green blue lightblue magenta} [
setpc :col fd 0.5 * (0.1 * (10 + repcount))
]
pu bk (0.5 * (7 * (0.1 * (10 + repcount))))
sr 1 fd 0.2 * (sin (0.5 * (repcount + 100)))
pd
]
END

TO redonpink
reset setpc 1 setbg 11 setbs -5
pu setfc 1
repeat 1000 [
setpos {-220 + random 440 -120 + random 240}
ra 0.001 setfo 50 setfs -15 + random 10
spot 5 + random 5
]
setorigin [-50 -30 2]
repeat 16 [
setmarkerwidth 3 home dropanchor
pullout 10 orbitleft repcount * 22.5
rt 180
repeat 70 [
setmarkerwidth markerwidth - 0.02
bk 0.1 mark 1 rt 2
]
repeat 70 [
setmarkerwidth markerwidth - 0.02
bk 0.1 mark 2 lt 2
]
]
END


TO roses
reset setpenwidth 5
repeat 3 [
pu setpos {-190 + (repcount * repcount) * 30 -90 + repcount * 50}
pd make "size 0.05 * (repcount / 2)
setpc item repcount [1 9 13]
repeat 9 [
repeat 100 [
fd repcount * :size rt 10
]
]
]
END


TO slats
reset
setorigin [-260 -120]
repeat 23 [
pu setps -7 + repcount
home sr 20 * repcount
setmarkerwidth 18 rt 10
mark 250
]
END


TO slats2
reset
setorigin [-260 -120]
repeat 23 [
pu setps -7 + repcount
home setpc pick [8 9 13]
sr 20 * repcount
setmarkerwidth 18 rt 10
mark 250
]
END

TO snake
CS PU RANDFC
BK 110 UP 90
repeat 80 [
cylinder 0.1 * repcount 1.6 10
sr sin (repcount * 10)
lo 1.5
]
repeat 60 [
cylinder 0.1 * (80 - repcount) 1.6 10
sr sin ((80 + repcount) * 10)
lo 1.5
]
DN 90 RT 60 ICOSPHEROID 5 2 SL 7 FD 3
RANDFC ICO 1 BK 6 ICO 1 HT
END

TO snakes
CS PU RANDFC
repeat 10 [
home setpos {-170 + (repcount * 30) -110}
up 90 repeat 80 [
cylinder 0.1 * repcount 1.6 10 sr sin (repcount * 10) lo 1.5
]
repeat 60 [
cylinder 0.1 * (80 - repcount) 1.6 10
sr sin ((80 + repcount) * 10) lo 1.5
]
DN 90 RT 60 ICOSPHEROID 5 2 SL 7 FD 3
RANDFC ICO 1 BK 6 ICO 1
]
HT
END

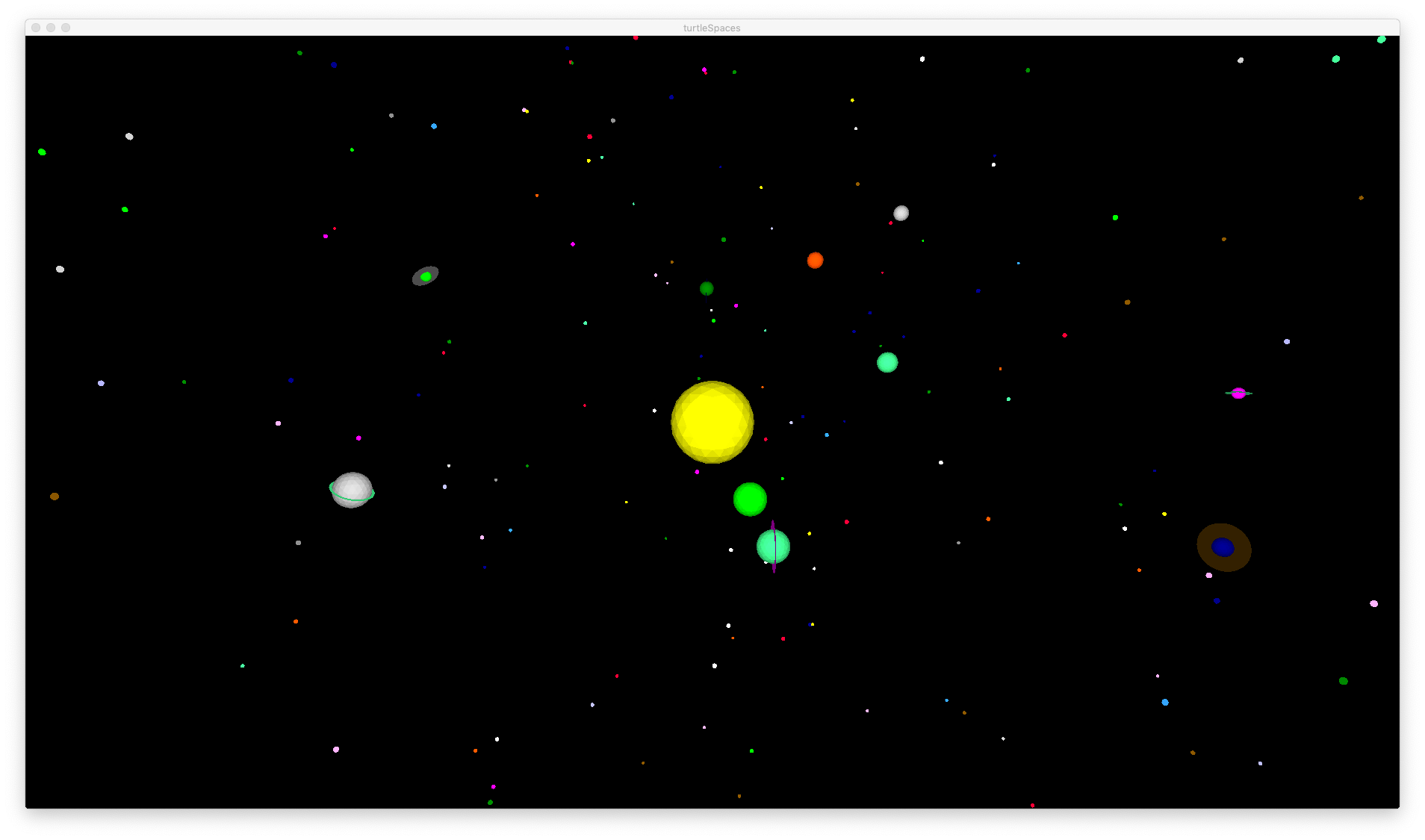
TO solar
reset repeat 5 [
setpc item repcount [1 8 9 13 15]
repeat 18 [
pu home raise 2 * repabove 1
rt repabove 1 rt repcount * 20
setps 0 pd mark 50
repeat 5 [
setps penshade + 1
repeat 90 [
mark 0.2 + 0.1 * repabove 1 rt 2
]
setpenshade penshade + 1
repeat 90 [
mark 0.2 + 0.1 * repabove 1 lt 2
]
]
]
]
END

TO solar2
reset setspeed 5
repeat 5 [
setpc item repcount [1 8 9 13 15]
repeat 18 [
pu home raise 2 * repabove 1
rt 3 * repabove 1
rt repcount * 20
setps 0 pd
mark 50
repeat 5 [
setps penshade + 1
repeat 90 [
mark 0.2 + 0.1 * repabove 1 rt 2
]
setpenshade penshade + 1
repeat 90 [
mark 0.2 + 0.1 * repabove 1 lt 2
]
]
]
]
END


TO solar3
reset setspeed 5
repeat 5 [
setpc item repcount [1 8 9 13 15]
repeat 18 [
pu home raise 2 * repabove 1
rt 4 * repabove 1
rt repcount * 20 setps 0
pd mark 50
repeat 5 [
setps penshade + 1
repeat 90 [
mark 0.2 + 0.1 * repabove 1
rt 2
]
setpenshade penshade + 1
repeat 90 [
mark 0.2 + 0.1 * repabove 1 lt 2
]
]
]
]
END

TO sparks
reset setpenwidth random 10
randbs randbg
repeat 5 [
pu setposition {-200 + random 400 -100 + random 200 -100 + random 100}
setorigin position randpc randps
repeat 30 [
rt random 360 pd
while (and xpos < 300 xpos > -300 ypos < 180 ypos > -180) [fd 1 lt 0.2]
pu home
]
]
END

TO spiralart
reset
snappy:pullin 100
pu
randbg
sl 40
rr 90
bk 10
repeat 2 [
randfc
repeat 2800 [
tube 2 repcount / 400 6
lo repcount / 500
up 2
]
pu home
fd 10 sr 40 rl 90
]
ht
END


TO spirallights
reset setpenwidth 5
repeat 5 [
make "ypos 130 - (40 * repcount)
randpc
repeat 10 [
pu setpos {-220 + (40 * repcount) :ypos}
pd
repeat 100 [
setps -10 + int (repcount / 5)
fd repcount / 10 rt 30
]
]
]
END

TO spirallightsorange
reset setbg 8
setbs 13 setpenwidth 5
repeat 5 [
make "ypos 130 - (40 * repcount)
repeat 10 [
pu setpc pick [1 8 9 13]
setpos {-220 + (40 * repcount) :ypos}
pd
repeat 100 [
setps -10 + int (repcount / 5)
fd repcount / 10
rt 30
]
]
]
END


TO spirallightsorange3d
reset setbg 8 setbs 13
setpenwidth 5
repeat 5 [
make "ypos 130 - (40 * repcount)
repeat 10 [
pu setpc pick [1 8 9 13]
setposition {-220 + (40 * repcount) :ypos 0}
pd
repeat 100 [
setps -10 + int (repcount / 5)
fd repcount / 10 rt 30 dn 2
]
]
]
END

TO splash
reset setspeed 5 setpenwidth 5
repeat 144 [
pu home rt repcount * 2.5 dn 75 pd
repeat 400 [
up 5 * (sin (repcount * 4))
setps -15 + (repcount / 12)
fd .4
]
]
pu home
END

TO splash2
reset setspeed 5 setpenwidth 5
repeat 144 [
pu home rt repcount * 2.5 dn 75 pd
repeat 400 [
up 5 * (sin (repcount * 4))
rt sin repcount
setps -15 + (repcount / 12)
fd .4
]
]
pu home
END

TO splash3
reset setspeed 5 setpenwidth 5
repeat 144 [
pu home rt repcount * 2.5 dn 75 pd
repeat 400 [
up 5 * (sin (repcount * 4))
rt sin repcount
rr sin repcount
setps -15 + (repcount / 12)
fd .4]
]
pu home
END

TO splash4
reset setspeed 5 setpenwidth 5 setpc 1
repeat 144 [
pu home rt repcount * 2.5 dn 75 pd
repeat 400 [
up 5 * (sin (repcount * 4))
rt sin repcount
rr sin repcount * 2
setps -15 + (repcount / 12)
fd .4]
]
pu home
END

TO spotwave
cs pu
repeat 32 [
setpos {-220 205 - (repcount * 10)}
repeat 45 [
setfc pick [2 3 5 6 7 10 14 15]
spot 5 sr 10
fd -2 + sin (repcount * 10)
]
]
END


TO stickman :size
lt 45 setmarkerwidth :size / 3
repeat 2 [
lt 90 mark :size * 5 spot :size
bk :size * 5] lt 135 mark :size * 2
lt 45 repeat 2 [
mark :size * 5 spot :size bk :size * 5 rt 90
]
lt 135 mark :size * 5
spot :size * 2 pu bk :size * 10
END
TO stickmen
reset pu sl 80 fd 20
repeat 3 [
randfc setpc fillcolor
stickman repcount * 3
pu sr 80 ra 20
]
END

TO stormy
reset pu setpos [-230 -120]
repeat 8 [
setpc item repcount [2 6 7 14 1 8 9 13]
repeat 160 [
pushturtle rt 45 bk random 20
randps mark 50 + random 20
popturtle pu
sr 2.5 + random 5 ra 0.01
]
ra 0.1 pu
setpos {-230 -120 + repcount * 30}
]
END

TO swirl
reset pu bk 20 sr 40 setpc 1
setbg 13 setbs -10 setorigin position pd
repeat 12 [
repeat 30 [
setropewidth 6.1 - (repcount / 5)
rope 4 bk 0.2 rt 6 bk 0.2
]
pu home rt repcount * 30 pd
]
ht
END


TO thicket3
reset setbg 2 setpenwidth 5 setpc 1
repeat 8 [
setpc item repcount [8 1 9 4 12 13 14 15]
repeat 20 [
pu setposition {-200 + (repcount * 20) 0 5 + repabove 1}
up 25 pd
repeat 80 [
fd 0.9 + ((repabove 2) * 0.1)
rt 8 * sin (repcount * 8)
]
lt 7.5
repeat 5 [
fd 20 pu bk 20 rt 15 pd
]
]
]
END

TO twomoons
reset
setorigin [-23 -23 0]
repeat 2 [
setpc item repcount [7 2]
repeat 36 [
pu home dropanchor
pullout 10 * repabove 1
orbitleft repcount * 10
rt 180 pd
if oddp repcount [fd 40 * repabove 1] [fd 20 * repabove 1]
]
setorigin [30 30 -20]
]
END


TO vase
reset setpenwidth 5 pu fd 50 sl 50 pd rt 135
repeat 40 [fd 1 rt 2]
repeat 125 [fd 1 lt 1]
lt 5 quad 80 220 rt 180 rr 180
quad 80 220 rr 180 rt 185
repeat 125 [fd 1 lt 1]
repeat 40 [fd 1 rt 2]
pu home bk 70 lt 15 setpc 15
repeat 6 [
pushturtle pd fd 150 + random 20
setfc pick [1 8 9 11] ra 0.1
spot 5 popturtle rt 6
]
END


TO weave
reset wrap
repeat 30000 [
fd 1 rt
sin repcount
if divisorp 1000 repcount [randpc]
]
END

TO zig
reset setbg pick [1 8 9 13]
setbs 10 setpenwidth 10
repeat 200 [
ra 0.1 pu
setpos {-220 + random 440 -120 + random 240}
rt random 360 setpc pick [1 8 9 13]
setps -15 + random 10
repeat 50 [
pd fd 50 + random 3 lt random 3 bk 50 + random 3
rt random 3 setps penshade + (-1 + random 3)
]
]
pu setpos [-100 -50]
setheading 300 pd setpc 1
setps 5 ra 1
repeat 15 [
bk 0.2 fd 20 rt 140
bk 0.2 fd 20 lt 132.5
]
END


TO zigzag
reset setbg 8 setbs 0 setpenwidth 5
repeat 360 [
pu home pd rt repcount * 1 lt 45
setpc pick [1 5 7 9]
repeat 20 [
fd repcount rt 90
fd repcount lt 90
]
]
END

TO zigzag3d
reset setbg 8 setbs 0 setpenwidth 5
repeat 360 [
pu home pd rt repcount * 1
lt 45 up 45 setpc pick [1 5 7 9]
repeat 20 [
fd repcount rt 90 fd repcount lt 90
]
]
END

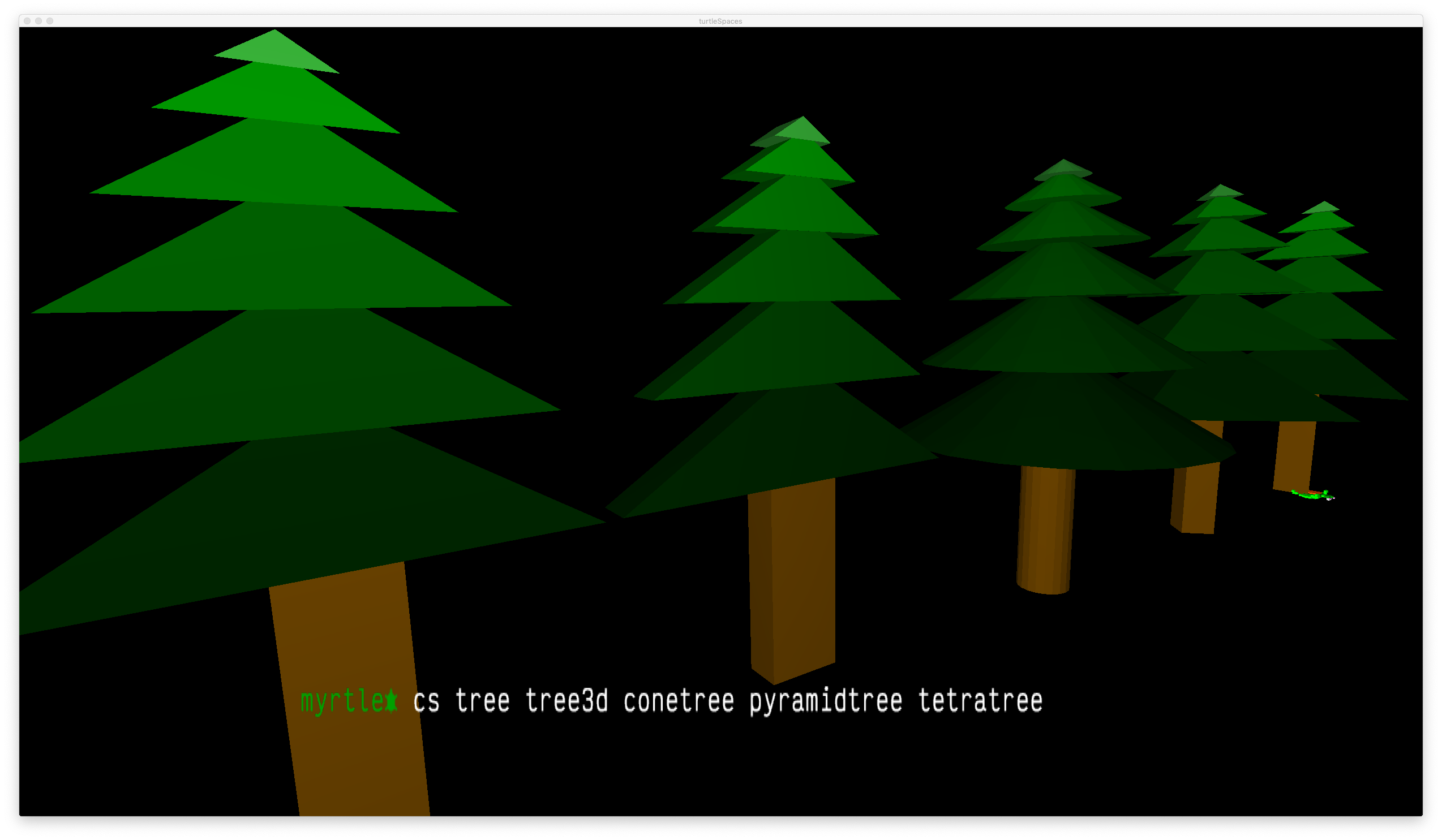
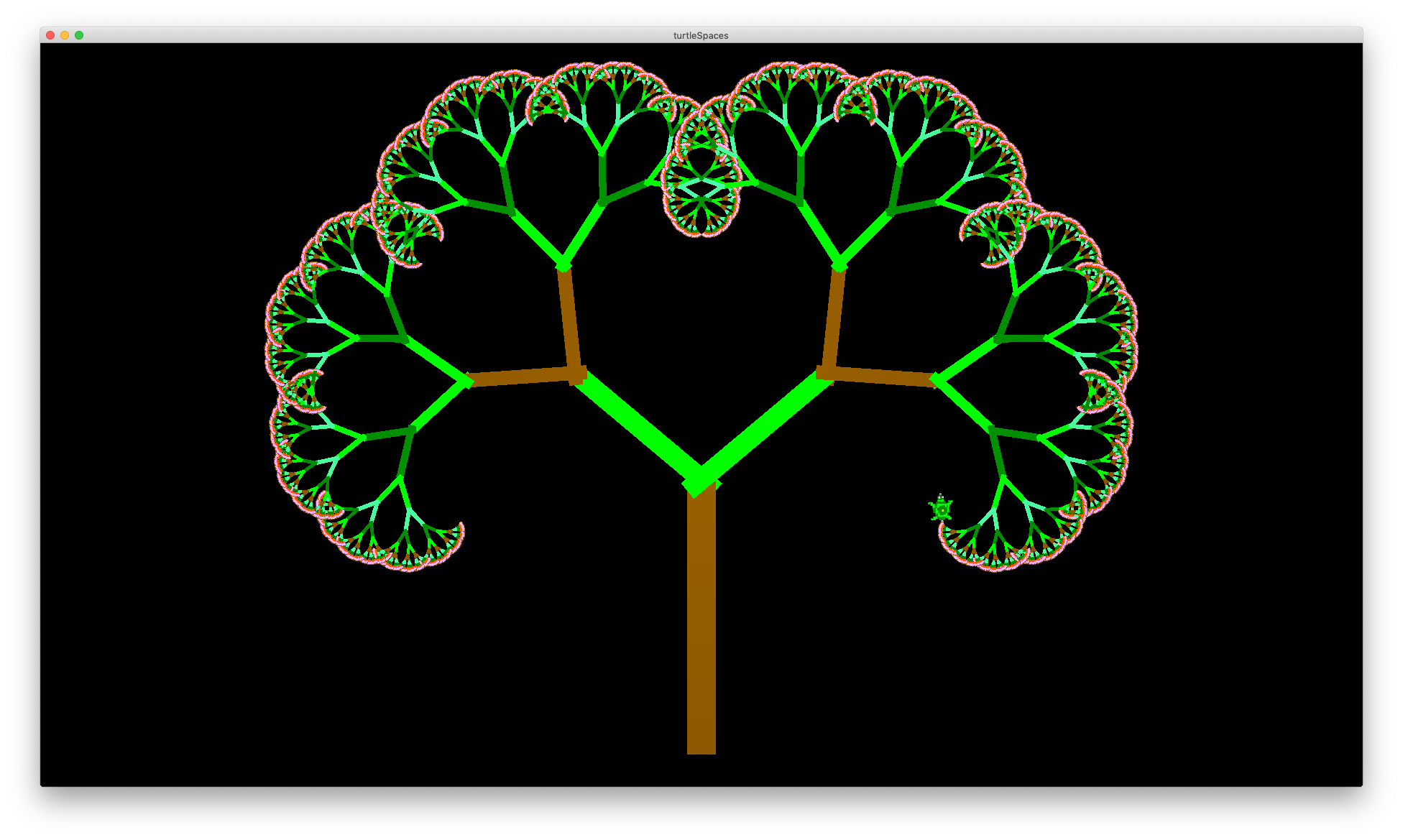
 TO tree
clearscreen penup
setpos [0 80] setfillcolor 4
repeat 6 [
setfillshade -6 + 3 * repcount
;repcount returns the current iteration
back 4 * repcount
fiso 8 * repcount 5 * repcount
;fiso = filled iso triangle
lower 0.1
]
setfillcolor 8 setfillshade 5
back 50 slideleft 10
quad 20 50
;trunk
END
TO tree
clearscreen penup
setpos [0 80] setfillcolor 4
repeat 6 [
setfillshade -6 + 3 * repcount
;repcount returns the current iteration
back 4 * repcount
fiso 8 * repcount 5 * repcount
;fiso = filled iso triangle
lower 0.1
]
setfillcolor 8 setfillshade 5
back 50 slideleft 10
quad 20 50
;trunk
END TO tree3d
cs pu setpos [0 80]
;cs = clearscreen
;pu = penup
setfc 4
;setfc = setfillcolor
repeat 6 [
setfs -6 + 3 * repcount
;setfs = setfillshade
bk 4 * repcount
;bk = back
tent 8 * repcount 5 * repcount 10
lo 0.1
;lo = lower
]
setfc 8 setfs 5
bk 50 sl 10
;sl = slideleft
voxeloid 20 50 10
;voxeloids are stretched cubes
END
TO tree3d
cs pu setpos [0 80]
;cs = clearscreen
;pu = penup
setfc 4
;setfc = setfillcolor
repeat 6 [
setfs -6 + 3 * repcount
;setfs = setfillshade
bk 4 * repcount
;bk = back
tent 8 * repcount 5 * repcount 10
lo 0.1
;lo = lower
]
setfc 8 setfs 5
bk 50 sl 10
;sl = slideleft
voxeloid 20 50 10
;voxeloids are stretched cubes
END TO conetree
cs pu setpos [0 80]
setfc 4 up 90
repeat 6 [
setfs -6 + 3 * repcount
ra 4 * repcount
cone 8 * repcount 5 * repcount 20
]
setfc 8 setfs 5 ra 50
cylinder 8 50 20
END
TO conetree
cs pu setpos [0 80]
setfc 4 up 90
repeat 6 [
setfs -6 + 3 * repcount
ra 4 * repcount
cone 8 * repcount 5 * repcount 20
]
setfc 8 setfs 5 ra 50
cylinder 8 50 20
END TO pyramidtree
cs pu setpos [0 80]
setfc 4 up 90
repeat 6 [
setfs -6 + 3 * repcount ra 4 * repcount
cone 8 * repcount 5 * repcount 4
;while there is also a pyramid primitive, you can
;also create a pyramid by creating a 4-sided cone
]
setfc 8 setfs 5 ra 50
cylinder 8 50 4
END
TO pyramidtree
cs pu setpos [0 80]
setfc 4 up 90
repeat 6 [
setfs -6 + 3 * repcount ra 4 * repcount
cone 8 * repcount 5 * repcount 4
;while there is also a pyramid primitive, you can
;also create a pyramid by creating a 4-sided cone
]
setfc 8 setfs 5 ra 50
cylinder 8 50 4
END TO tetratree
cs pu setpos [0 80] setfc 4 up 90
repeat 6 [setfs -6 + 3 * repcount
ra 4 * repcount
cone 8 * repcount 5 * repcount 3]
setfc 8 setfs 5 ra 50
cylinder 8 50 3
END
TO tetratree
cs pu setpos [0 80] setfc 4 up 90
repeat 6 [setfs -6 + 3 * repcount
ra 4 * repcount
cone 8 * repcount 5 * repcount 3]
setfc 8 setfs 5 ra 50
cylinder 8 50 3
END